
Fonte: Shutterstock.
Áudio disponível no material digital.
Praticar para aprender
Caros estudantes, estamos iniciando a terceira e última seção da unidade de bioestatística. Nela vamos aprofundar ainda mais nossos conhecimentos sobre as medidas de dispersão e sobre a probabilidade, além de estudar sobre os principais conceitos dos testes de hipótese.
Partiremos dos conhecimentos já adquiridos até aqui sobre estatística descritiva dos dados e avançaremos no estudo da estatística inferencial, aquela que nos permite tirar conclusões sobre características de uma população a partir de uma amostra.
Assim, iniciaremos a seção apresentando o conceito e a aplicabilidade dos quartis, demonstrados com exemplos para melhor compreensão. Adiante, trataremos das medidas de dispersão: amplitude, variância, desvio padrão e coeficiente de variação, conceitos fundamentais que nos permitem conhecer melhor um conjunto de dados para além das medidas de posição já vistas até aqui. Outros pontos abordados serão o cálculo de probabilidade básico e os conceitos sobre intervalo de confiança. Por fim, os conceitos gerais de teste de hipótese e alguns dos principais testes estatísticos utilizados pela área da saúde serão descritos.
Novamente, todos os assuntos serão amplamente exemplificados e contextualizados para melhor compreensão e internalização. Bons estudos!
Tomando como base os conteúdos apresentados nesta seção, vamos imaginar uma situação hipotética na qual um grupo de gestores e profissionais da saúde de um município do Sudeste brasileiro se reúne para averiguar os resultados de testes que avaliaram o conhecimento sobre medidas de prevenção contra a Covid-19 em usuários idosos, com capacidade cognitiva preservada, de duas instituições de longa permanência (instituições A e B).
Os integrantes desse grupo decidiram que a nota 6,0 seria a média considerada desejável e obtiveram os seguintes resultados:
Média das notas dos idosos da instituição A: 6,0
Média das notas dos Idosos da instituição B: 6,0
Os gestores e profissionais envolvidos ficaram satisfeitos com os resultados, considerando o perfil da população, e atribuíram os resultados positivos a programas de educação em saúde promovidos pelo município. Concluíram, portanto, que as medidas educativas haviam sido suficientes e que não havia necessidade de outras intervenções em nenhuma das instituições. Você, profissional que acaba de se juntar à equipe, concorda com os demais membros do grupo?
Para auxiliá-lo na decisão, estão adiante as notas de cada um dos idosos das duas instituições.
| Notas dos idosos da instituição A | Notas dos idosos da instituição B |
|---|---|
| 7 | 10 |
| 5 | 2 |
| 6 | 2,5 |
| 5,5 | 3 |
| 6,5 | 9,5 |
| 8 | 1,5 |
| 4 | 9 |
| 6 | 6,5 |
| 7 | 10 |
| 5 | 6 |
| = 6 | = 6 |
Estamos chegando ao final da unidade de bioestatística e você, futuro profissional, estará pronto para utilizar mais esta ferramenta em sua jornada profissional para fazer a diferença!
conceito-chave
Medidas separatrizes: quartis, decis e percentis
Os quartis são observações ou medidas de localização que dividem o rol (a sequência ordenada de dados) em quatro partes de igual valor, as quais são, portanto, apresentadas em primeiro, segundo e terceiro quartil ou Q1, Q2 e Q3, respectivamente.
Há também os decis, que dividem o rol em dez partes iguais, e os percentis, que o dividem o rol em cem partes iguais.
A partir de agora, direcionaremos nossos estudos para os quartis, valores dados a partir de uma série de elementos dispostos em ordem crescente, que dividem a distribuição em partes iguais. Sendo: Q1 = número que deixa 25% abaixo e 75% acima; Q2 = será sempre igual à mediana, deixa 50% das observações abaixo e 50% acima; e Q3 = número que deixa 75% das observações abaixo e 25% acima.
Para melhor compreensão vamos acompanhar o seguinte exemplo:
A variável peso, de pacientes internados em uma clínica médica, é representada a seguir:
Rol: 73 – 74 – 77 – 52 – 85 – 59 – 73 – 84 – 92
A partir desse conjunto vamos determinar os quartis (Q1, Q2 e Q3):
1º passo: devemos organizar o nosso rol de observações em ordem crescente.
Rol: 52 – 59 – 73 – 73 – 74 – 77 – 84 – 85 – 92
2º passo: note que esse conjunto apresenta número ímpar de dados. Agora, deveremos identificar o valor central dele, o que, nesse caso, fica fácil, já que é um conjunto com poucos elementos, mas, para conjuntos maiores, você deverá somar o número total de elementos do conjunto (nesse caso 9) + 1 e dividir por 2, o resultado dará a posição em que o valor central se encontra, ou seja, 9+1 = 10/2= 5. Logo o valor na quinta posição do conjunto representa o valor central.
Rol: 52 – 59 – 73 – 73 – 74 – 77 – 84 – 85 – 92
Lembre-se de que o segundo quartil (Q2) é igual à mediana, logo podemos dizer que Q2 = 74.
3º passo: para calcular Q1 e Q2, é necessário calcular a mediana à direita e à esquerda do conjunto. Para tal, deve-se identificar os valores centrais novamente e fazer o cálculo da mediana.
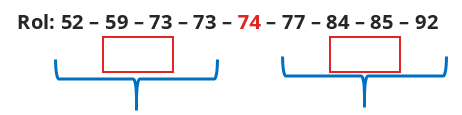
Q1 = 59+73/2 = 122/2 = 66
Q2 = 74
Q3 = 74
Caso o conjunto seja formado por um número par de elementos, para conhecer a mediana (Q2), deve-se somar os dois números centrais e dividir por dois.
Exemplo:
Rol: 52 – 59 – 73 – 73 – 74 – 77 – 84 – 85 – 92 – 93
Como o conjunto em questão possui dez elementos, deveremos descobrir Q2 somando os dois valores centrais, que serão divididos por 2.
Rol: 52 – 59 – 73 – 73 – 74 – 77 – 84 – 85 – 92 - 93
Q2 = 74+77/2= 75,5.
Como pudemos observar, nem o elemento 74, nem o 77 representam a mediana, logo eles deverão ser considerados para encontramos os quartis restantes (Q1 e Q3).
Rol: 52 – 59 – 73 – 73 – 74 – 75,5 – 77 – 84 – 85 – 92 - 93
Agora é só identificar o valor central à esquerda e à direita!
Rol: 52 – 59 – 74 – 73 – 74 – 75,5 – 77 – 84 – 85 – 92 - 93
Resultados para o conjunto com número par de elementos serão:
Q1 = 73
Q2 = 75,5
Q3 = 85
Medidas de dispersão
Como já vimos na seção anterior, para que seja possível caracterizar adequadamente uma série de dados, é necessário expressar as tendências do conjunto em números ou estatísticas. Para tal, utilizamos as medidas de posição, já apresentadas, e as medidas de dispersão.
As medidas de dispersão auxiliam as medidas de tendência central a melhor descrever a série de dados, pois é capaz de identificar a distância que os elementos de um conjunto estão uns dos outros. Logo, podemos dizer que a finalidade das medidas de dispersão é encontrar um valor que seja capaz de resumir a variabilidade de um conjunto de dados.
Assimile
É importante compreender que a média aritmética de um conjunto de dados cuja dispersão é muito grande não apresentará uma representatividade adequada do conjunto observado. Logo, temos as medidas de dispersão que melhor representarão essa série de dados.
Exemplo: em um conjunto de dados hipotético, dois grupos se apresentam: Grupo 1: -10, 0, 10, 20, 30
Grupo 2: 8, 9, 10, 11, 12
Ao calcularmos a média aritmética dos dois conjuntos, encontramos o valor 10. Porém se observarmos os elementos de cada um deles, veremos que há uma variação ou uma distância muito maior entre os valores e o valor central no Grupo 1 do que no Grupo 2.
Dessa forma, para compreendermos melhor essas séries de dados, é necessário calcular as medidas de dispersão, como variância e desvio padrão.
Com o intuito de que você compreenda melhor, vamos tomar como exemplo a seguinte série de dados:
| Boletim | Notas Aluno A | Notas Aluno B |
|---|---|---|
| Biologia | 7 | 7,5 |
| Português | 10 | 6 |
| História | 6 | 7 |
| Física | 8 | 6,5 |
| Matemática | 4 | 8 |
É possível notar uma variabilidade diferente entre os elementos de cada conjunto (alunos A e B), porém, quando calculamos a média aritmética, encontramos valor igual: ambos têm média geral 7 entre todas as matérias, como podemos ver nos cálculos abaixo.
Média do Aluno A = = 7
Média do Aluno B = = 7
É possível notar que o Aluno A apresentou maior variabilidade nas notas para alcançar a média 7, já o Aluno B alcançou a mesma média com notas mais uniformes.
Então, nesse caso, o que poderemos fazer para melhor diferenciar essas duas distribuições? Utilizaremos esse exemplo para explicar: amplitude, variância e desvio padrão.
Amplitude: uma das formas de medir a dispersão de um conjunto de dados. A amplitude de uma série de dados é representada pela diferença entre o maior e o menor elemento do conjunto, ou seja, consiste em, basicamente, subtrair o menor elemento do maior.
Tomando como base o exemplo da média dos alunos A e B, temos:
Amplitude:
Aluno A: 10 – 4 = 6
Aluno B: 8 – 6 = 2
Note que a amplitude dos dados do Alunos A é maior que a do B, logo podemos dizer que os dados (ou notas) do Aluno A estão mais dispersos do que os do Aluno B, em relação à média.
Essa medida, no entanto, dá-nos apenas noção da distância entre o menor e o maior valor do conjunto. Para entender melhor a dispersão entre os elementos, falaremos sobre a variância e o desvio padrão.
Variância: é uma medida de dispersão que demonstra quão distante cada elemento do conjunto está do valor central ou média. A variância é representada pelo símbolo sigma ao quadrado (σ2). Para calculá-la é preciso seguir as etapas adiante:
-
É necessário, primeiramente, identificar a média do conjunto de dados. Nesse caso, como estamos seguindo o mesmo exemplo das notas dos Alunos A e B, temos média 7.
Média do Aluno A = = 7
Média do Aluno B = = 7
-
Verificar a diferença entre cada um dos elementos com relação à média, ou seja, subtrair os elementos do valor da média e elevá-los ao quadrado.
Variância = =
Continuando:
Variância = = 4
-
Agora deve-se calcular uma segunda média. Para tal, basta dividir os valores encontrados ao elevar cada um dos elementos ao quadrado pelo número de elementos do conjunto.
Variância = = = 4
A variância () do conjunto de notas referentes ao Aluno A será igual a 4.
Exemplificando
Vamos tomar como exemplo extra o cálculo da variância das notas do Aluno B.
Já sabemos que a média é a mesma que a do Aluno A, ou seja, 7.
Vamos ao segundo passo então:
Variância = =
Calculemos as diferenças entre cada elemento e as médias:
Variância = =
Em seguida, elevemos as diferenças encontradas ao quadrado:
Variância = = = 0,5
A variância () do conjunto de notas referentes ao Aluno B será igual a 0,5.
Logo, pelos resultados apresentados, podemos dizer que as notas do Aluno B apresentam menor variância, o que significa que os elementos estavam mais próximos do valor central do que as notas obtidas pelo Aluno A.
Desvio Padrão (DP): representa a uniformidade ou o grau de dispersão de determinado conjunto de dados. Quanto mais próximo esse valor for de zero, maior será a homogeneidade dos dados.
Para calcularmos o DP dos dados, devemos encontrar a raiz quadrada da variância.
DP do Aluno A =
DP do Aluno B = Ou seja, embora ambos tenham alcançado a mesma média geral, encontramos valores diferentes de variação entre os conjuntos.
Podemos dizer, então, que, em média, as notas do Aluno A se afastaram 2 pontos ou duas unidades, para cima ou para baixo, em relação à média.
O DP resultante das médias do Aluno B demonstra que houve menor variação em torno da média, sendo, aproximadamente, 0,71 unidades para cima ou para baixo em relação à média.
Coeficiente de variação: é também conhecido como Desvio Padrão Relativo e é interpretado como a variabilidade dos dados em relação à média, sendo expresso usualmente em porcentagem. Quanto menor o coeficiente de variação, mais homogêneo são os dados do conjunto.
Para exemplificarmos isso, tomaremos ainda o mesmo exemplo das notas dos Alunos A e B.
Nesse caso, já temos todos os valores de que necessitamos para o cálculo, sendo eles o Desvio Padrão e a média, bastando agora apenas substituí-los na fórmula e operacionalizarmos o cálculo.
Fórmula:
CV do Aluno A = = = 28,57 ou 28,6
CV do Aluno B = = =
Os resultados mostram, mais uma vez, que as notas do Aluno B apresentaram menor variação em relação à média, sendo a taxa identificada de 10,14%, enquanto o Aluno A apresentou coeficiente de variação mais elevado (28,57%).
Probabilidade
É o ramo matemático que se dedica ao cálculo das chances de ocorrência de um fenômeno ou experimento, como a probabilidade de se obter cara ou coroa no lançamento de uma moeda ou, ainda, a chance de se tirar seis em uma rolagem de um dado com seis faces.
Para compreender melhor probabilidade é necessário conceituar alguns termos amplamente utilizados em seu estudo.
Espaço amostral: representado pela letra ômega (Ω), é definido como o conjunto de todos os possíveis resultados de um experimento. Exemplo: ao lançar um dado não viciado, o espaço amostral (Ω) será igual ao conjunto: 1, 2, 3, 4, 5, 6, pois estes são os possíveis resultados de um dado com seis faces.
Evento: é o resultado esperado, ou seja, o evento que se quer investigar. Exemplo: ao rolar um dado, qual a probabilidade de se obter um resultado acima de 4? Nesse caso o evento será representado por uma letra maiúscula A = 5, 6. Estes seriam os possíveis resultados acima de 4, ou seja, o evento que se deseja investigar é a chance dessa ocorrência.
Fórmula:
Probabilidade (P) = ou seja,
Parte ou resultados favoráveis: são aqueles resultados favoráveis à sua pergunta, ou seja, em nosso exemplo, desejamos saber qual a probabilidade de se obter acima de 4 em um dado. Sabemos que acima de 4 há os valores 5 e 6, ou seja, há dois resultados possíveis para o evento desejado.
Todo ou resultados possíveis: são todos os resultados possíveis de se obter em um dado. Nesse caso temos 6 resultados possíveis (podemos obter os resultados 1, 2, 3, 4, 5 e 6).
Probabilidade (P) = e simplificando por 2 temos
A probabilidade pode ser expressa não só por número fracionário, mas também por números decimais. Nesse caso, . Ou pode ser expresso, ainda, em taxa decimal, multiplicando-se o valor por 100 33,3%.
Intervalo de confiança
O intervalo de confiança (IC) é utilizado para indicar a confiabilidade de uma estimativa. Como já vimos em outras seções, a maioria dos estudos científicos utilizam amostras populacionais para responder seus questionamentos, já que estudar populações inteiras inviabilizaria a maioria dos protocolos de pesquisa, seja pela logística de coleta de dados, seja pela escassez de recursos humanos e/ou materiais para sua realização. A questão que surge é: como assegurar que a amostra selecionada refletirá as características que queremos observar na população-alvo?
Esse questionamento é legítimo, pois muitos cuidados devem ser tomados no momento da seleção da amostra, questão também já discutida nas seções anteriores. Nesse sentido, a estatística apresenta ferramentas capazes de minimizar a possibilidade desse tipo de erro, dentre elas discutiremos mais a fundo o IC.
O IC diz respeito ao nível de confiança, por meio de uma estimativa para um parâmetro populacional, obtido a partir de elementos amostrais, os quais se espera que contenham o valor do parâmetro populacional com um nível de confiança que, geralmente, vai de 90 a 99%.
É importante ressaltar o risco de erro na construção de um intervalo de confiança. Por exemplo, se o nível de confiança é de 95%, o risco de erro da inferência estatística será de 5%.
Exemplificando
Caso o intervalo de confiança escolhido seja o de 95%, isso significará que, se averiguássemos a variável de interesse em 100 amostras diferentes da mesma população (por exemplo a média de altura ou de peso dos habitantes), 95 dessas amostras conteriam o parâmetro populacional, ou seja, refletiriam as reais características daquela população, e as outras cinco amostras não conteriam o parâmetro.
Há vários cálculos para o IC, mas vamos focar no cálculo para a média, o qual pode ser usado para conhecer o desvio padrão populacional ou para amostras grandes com trinta ou mais elementos.
Fórmula do cálculo do IC para média:
Sendo:
= a média.
Zc = Z crítico é representado por valores disponíveis na tabela de distribuição normal padrão, sendo os valores mais utilizados os de 1,96 para 95% de confiança; 1,64 para 90% de confiança; e 2,57 para 99% de confiança. São valores padrão.
σ = Desvio Padrão Populacional.
= tamanho da amostra.
Exemplo de cálculo:
Tem-se uma amostra de 100 participantes e encontra-se uma média de 24 anos entre os participantes. Sabendo que a variância das idades é de 16 anos, construa um intervalo de 95% de confiança para a média.
- É necessário compreender que, neste caso, o que estamos fazendo é calcular a margem de erro para a média.
-
Calcular a margem de erro, representado pela letra E.
Substituímos os valores:
Note que o exemplo apresenta apenas a variância das idades, que é 16, porém não há o valor do Desvio Padrão (DP). Sabemos, no entanto, que o DP é igual a raiz quadrada da variância. Sendo a variância 16, podemos dizer, então, que o DP é igual a 4.
O valor de Z crítico será 1,96, pois o intervalo de confiança pedido foi de 95%. Sendo a amostra composta por 100 participantes, logo teremos: -
Efetuar o cálculo da margem de erro:
-
Apresentar o resultado para o intervalo de 95%:
Vamos relembrar que a fórmula do IC, que nada mais é que a média, mais ou menos a margem de erro, parte da fórmula representada anteriormente.Logo: anos
Assim sendo, pode-se concluir que esse intervalo está, mais ou menos, 0,784 a partir da média 24, entre 23,216 e 24,784, para IC de 95%.
Testes de hipótese
Consiste em uma metodologia que auxilia na tomada de decisão sobre uma ou mais populações obtidas a partir de informações extraídas de uma amostra por meio de inferência estatística. É a partir do teste de hipótese que podemos avaliar a veracidade de um ou mais parâmetros populacionais.
Para realizar o teste de hipótese, inicialmente, devemos admitir um valor hipotético para um parâmetro populacional, o qual pode ser a variável altura, peso ou qualquer outro parâmetro que se deseja observar na população e que pode ser obtido a partir de uma amostra. Com base nas informações dessa amostra, é feito um teste estatístico que aceitará ou rejeitará esse valor hipotético assumido.
Reflita
É importante atentar-se para o fato de que a decisão de aceitar ou rejeitar uma hipótese a partir de elementos coletados de uma amostra sempre apresentará risco de erro, ou seja, jamais será definitivamente correta. Porém, é possível dimensionar a probabilidade (risco) da decisão de aceitar ou rejeitar a hipótese. Lembre-se sempre de que, quando se tenta inferir algo sobre uma população a partir de uma amostra, tem-se a possibilidade de erro estatístico ainda que se assuma um erro mínimo de 1% ou de 5%. O erro será zero apenas quando se trabalhar com toda a população, o que, na maioria das vezes, é inviável ou impossível.
Em que momento podemos aplicar tais ferramentas em um estudo de população dentro do contexto da saúde pública?
Para que seja possível testar um parâmetro populacional, é necessário afirmar um par de hipóteses. Uma hipótese deverá representar a afirmação do parâmetro e a outra seu complemento. Dessa forma, quando uma das hipóteses for falsa, a outra automaticamente será verdadeira. Elas são chamadas de hipótese nula e hipótese alternativa.
Hipótese nula (): hipótese estatística que possui uma afirmação de igualdade, como menor ou igual, igual ou maior ou igual (, = ou ).
Hipótese alternativa (): é o complemento da hipótese nula. Será verdadeira caso a outra seja falsa e vice-versa. Contém afirmação de desigualdade estrita, como menor, diferente ou maior (<, ≠ ou >).
Exemplo:
= a letra grega “mi” representa, em estatística, a média populacional.
K= representa um número real.
A hipótese nula diz que a média populacional é igual a K, já a hipótese alternativa diz que a média populacional é diferente de K. É importante observar que esse contraste sempre ocorrerá entre as hipóteses, pois uma sempre deverá ser o oposto complementar da outra, ou seja, se a hipótese nula é falsa, a alternativa é sempre verdadeira e também o contrário é verdadeiro.
Para visualizarmos melhor o exemplo, imaginemos que estamos avaliando a média de altura populacional. Vamos tomar como valor hipotético a altura de 1,65, obtida a partir de uma amostra dessa população.
Logo, poderíamos supor que a hipótese nula diz que a média de altura da população é igual ou menor que 1,65. A hipótese alternativa será de que a média de altura da população é superior a 1,65.
No processo de aceitar ou refutar uma hipótese, podem ocorrer alguns tipos de erros, denominados: Erro Tipo I (α) e Erro Tipo II (β).
Erro Tipo I: é o erro de rejeitar , sendo verdadeira.
Erro Tipo II: é o erro de aceitar , sendo falsa.
Logicamente, o objetivo do tomador de decisões é diminuir, ao mínimo, a probabilidade de ocorrência dos dois tipos de erros. Porém, à medida que a probabilidade de ocorrência do Erro Tipo I diminui, aumenta a probabilidade do Erro Tipo II e vice-versa.
A única forma de diminuir o risco dos dois tipos de erros simultaneamente é aumentando o tamanho da amostra, porém, como já falamos, isso nem sempre é possível.
Fórmula de teste de hipótese para média populacional com variância conhecida:
= a média amostral
= a média populacional testada (sob )
σ = Desvio Padrão Populacional
√n = raiz quadrada do tamanho da amostra
Testes T: são testes de hipótese utilizados para comparar as médias de uma amostra com uma população, comparar duas amostras pareadas ou duas amostras independentes.
E assim chegamos ao fim de mais uma unidade. É hora de revisarmos todos os conceitos e compreendermos a forma como cada assunto se relaciona com as outras áreas e com nossa prática profissional. A bioestatística é uma ciência rica e complexa que se relaciona com todos os saberes e é ferramenta indispensável para a manutenção e para a proteção à saúde em nossa sociedade.
Faça valer a pena
Questão 1
Em um relatório mensal, analistas da Receita Federal perceberam que um contribuinte em particular apresentava o maior desvio padrão de toda a base de dados com relação aos valores pagos em impostos se comparado aos demais contribuintes.
Assinale a alternativa que apresenta a afirmação correta com relação à situação apresentada:
Tente novamente...
INCORRETA, pois o desvio padrão representa quão dispersos estão os dados em relação à média, logo esse contribuinte estaria pagando mais ou menos que a média dos contribuintes.
Tente novamente...
INCORRETA, pois o desvio padrão representa quão dispersos estão os dados em relação à média, logo esse contribuinte estaria pagando mais ou menos que a média dos contribuintes.
Tente novamente...
INCORRETA, pois houve alguma variação, seja para mais ou para menos.
Correto!
CORRETA, pois o desvio padrão muito significativo indica que esses valores estavam bem abaixo ou acima da média dos outros contribuintes, logo estavam dispersos.
Tente novamente...
INCORRETA, pois o desvio padrão indica valores dispersos em relação à média, não necessariamente duplicados.
Questão 2
A variância é definida como uma medida de dispersão que demonstra quão distante cada elemento do conjunto está do valor central ou média, sendo muito utilizada, junto à medida de desvio padrão, por melhor caracterizar um conjunto de dados, se comparados à média aritmética simples.
Com relação ao conceito de variância e de desvio padrão, assinale a alternativa correta:
Tente novamente...
INCORRETA, pois a variância é igual ao somatório dos quadrados das diferenças entre cada observação e a média aritmética delas, cujo resultado é dividido pelo número de observações.
Tente novamente...
INCORRETA, pois a variância é igual ao somatório dos quadrados das diferenças entre cada observação e a média aritmética delas, cujo resultado é dividido pelo número de observações.
Tente novamente...
INCORRETA, pois a variância é igual ao somatório dos quadrados das diferenças entre cada observação e a média aritmética delas, cujo resultado é dividido pelo número de observações.
Tente novamente...
INCORRETA, pois é a raiz quadrada da variância que indica o desvio padrão.
Correto!
CORRETA, pois a raiz quadrada da variância indica o valor do desvio padrão do conjunto.
Questão 3
Os cálculos de dispersão são essenciais para melhor caracterizar um conjunto de dados e até mesmo para compará-los. Os dados a seguir são as quantidades de agentes de saúde em cinco unidades de saúde: 6, 5, 8, 5, 6.
Assinale a alternativa que representa a variância e o desvio padrão (DP) da quantidade de agentes de saúde dessas cinco unidades.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A alternativa correta é: Variância de 1,2 e DP 1,1.
Resolução do cálculo:
Inicialmente calcula-se a média do conjunto: 6 + 5 + 8 + 5 + 6/5 =30/5 = 6
Depois devemos calcular a variância:
Por fim, para obter o desvio padrão, devemos fazer a raiz quadrada da variância: = 1,1
Logo, o resultado para variância será 1,2 e para desvio padrão será 1,1.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
BUSSAB, W. O.; MORETTIN, P. A. Estatística básica. 9. ed. São Paulo: Saraiva, 2017. E-book.
CALLEGARI-JAQUES, S. M. Bioestatística: princípios e aplicações. Porto Alegre: Artmed, 2007. E-book.
CARVALHO, S.; CAMPOS, W. Estatística básica simplificada. Rio de Janeiro: Juspodivm, 2016.
FEIJOO, A. M. L. C. de. Medidas de tendência central. In: FEIJOO, A. M. L. C. de. A pesquisa e a estatística na psicologia e na educação. Rio de Janeiro: Centro Edelstein de Pesquisas Sociais, 2010. p. 14-22. Disponível em: https://bit.ly/2TrR3VM. Acesso em: 10 jan. 2021.
GUEDES, T. A.; JANEIRO, V.; MARTINS, A. B. T.; ACORSI, C. R. L. Estatística descritiva. In: GUEDES, T. A.; JANEIRO, V.; MARTINS, A. B. T.; ACORSI, C. R. L. Projeto de Ensino: aprender fazendo estatística. [S. l.: s. n.], 2005. Disponível em: https://bit.ly/35ql7U9. Acesso em: 18 jan. 2021.
MAGALHÃES, M. N.; LIMA, A. C. P. Noções de Probabilidade e Estatística. São Paulo: EDUSP, 2008.
REIS, E. A., REIS I. A. Análise Descritiva de Dados. Relatório Técnico do Departamento de Estatística da UFMG. Belo Horizonte: UFMG, 2002. Disponível em: https://bit.ly/3cFjciQ. Acesso em: 10 jan. 2021.



