Noções básicas de estatística

Fonte: Shutterstock.

Áudio disponível no material digital.

Convite ao estudo

Prezado estudante, nesta unidade aprofundaremos nossos saberes a respeito dos conceitos e das ferramentas da bioestatística, disciplina essencial para diversas áreas do conhecimento, principalmente para os profissionais da área da saúde.
Inicialmente, serão apresentados os conceitos básicos e introdutórios da estatística e a sua aplicação na área da biologia e da saúde, a bioestatística. 
Em um segundo momento, abordaremos as bases da estatística descritiva, sua aplicabilidade, os conceitos importantes para sua interpretação (média, frequências, desvio médio, dispersão) e suas formas de apresentação, que podem ocorrer em gráficos e tabelas por exemplo. Tais conceitos são amplamente aplicados em estudos científicos da área da saúde, além de apontarem outros indicadores de saúde na prática clínica.
Na terceira e última seção, estudaremos a probabilidade, outra ferramenta estatística importante e amplamente utilizada. Os conceitos abordados serão: probabilidade, mediana, média, desvio padrão e testes utilizados para comprovar ou refutar hipóteses, além de outros instrumentos da bioestatística.
A compreensão desses saberes complementa o conteúdo contemplado na disciplina até aqui e fornece ferramentas essenciais para enfrentar situações-problema nas áreas das ciências biológicas. Portanto, todos os critérios de coleta, organização e análise de dados serão apresentados e detalhados à luz dos principais métodos estatísticos. Bons estudos!

Praticar para aprender

Prezados acadêmicos, iniciamos a primeira seção da Unidade 4. Nesta etapa construiremos e aperfeiçoaremos saberes a respeito dos conceitos e das ferramentas da bioestatística, disciplina fundamental para os profissionais da área da saúde.
Inicialmente, serão abordados os conceitos gerais da estatística e serão apresentadas suas principais vertentes. Além disso, veremos os primeiros registros históricos da utilização dessa ciência amplamente empregada por todas as áreas do conhecimento.
Em um segundo momento, conceituaremos os principais termos utilizados na área, como o que é população, amostra, dado, variável e suas subdivisões. Compreender esses termos-chave é muito importante para a compreensão e a utilização dos métodos, em bioestatística, pelos profissionais da saúde.
Trataremos ainda dos tipos de variáveis quantitativas e qualitativas e os tipos de escalas existentes com diversos exemplos para fixar o conhecimento e facilitar a compreensão. 
Para encerrar a seção, abordaremos os principais tipos de amostragem, suas aplicações, vantagens e desvantagens, além de discutirmos sobre a importância da formação do tamanho amostral de um estudo, desde a quantidade adequada de participantes até a adequação deles ao estudo, para que expressem a característica que se quer investigar, e a problemática das amostras tendenciosas e suas consequências.
Considerando os conteúdos desta seção sobre os conceitos básicos de amostragem, vamos acompanhar um grupo de pesquisadores que deseja realizar um estudo sobre a presença de doenças crônicas em trabalhadores da indústria têxtil de uma cidade do Sudeste do Brasil.
Os estudiosos desenvolvem, então, o projeto para essa pesquisa e o encaminham ao Comitê de Ética do Hospital Central (grupo composto por diversos representantes especialistas e membros da sociedade que avaliam a pertinência do projeto) para que ele avaliasse o estudo e aprovasse ou não o projeto. Dois meses se passam e o trabalho retorna, sem aprovação, para que os pesquisadores realizem alterações em seu método. No item “Amostra” há uma observação que questiona a utilização de uma amostra por conveniência e que indaga o motivo dos dados serem coletados em apenas uma das oito fábricas do ramo na cidade e o fato de não existir nenhum cálculo amostral para se definir o tamanho da amostra. Você, enquanto pesquisador do grupo, concordaria com as observações feitas pelo Comitê de Ética? Quais as possíveis soluções para essa questão metodológica?
Compreender os conceitos e termos-chave de bioestatística permite ao futuro profissional da saúde ser suficientemente capaz de desenvolver estudos científicos para investigar problemas que atingem a população e para propor possíveis soluções às questões identificadas. Bom estudo a todos!

CONCEITO-CHAVE

Introdução à estatística e à bioestatística

Os primeiros registros encontrados sobre a utilização da estatística são relatos de Confúcio sobre levantamentos feitos na China e datam de 2.000 anos antes da era cristã. Outras civilizações antigas, como a dos egípcios, e civilizações pré-colombianas (incas, maias e astecas), também utilizaram informações estatísticas, segundo estudos arqueológicos. 
Dessa maneira, podemos compreender que, desde a Antiguidade, dados estatísticos com informações populacionais e de riquezas eram utilizados pelos governantes para decidir sobre suas ações e movimentos políticos, principalmente nas áreas tributária e militar.
Essa prática tornou-se indispensável e, até os dias de hoje, é amplamente utilizada, não só para questões econômicas e militares, mas para todos os outros setores, como os sociais, os educacionais e também na área da saúde.

A palavra “estatística” deriva da palavra latina status, que, originalmente, era compreendida como “informações úteis ao Estado”, ou seja, as questões relacionadas à composição demográfica, aos recursos, às taxações, etc. Pode-se conceituar estatística, então, como a ciência que coleta, organiza e analisa dados quantitativos, de forma que seja possível julgá-los ou interpretá-los racionalmente.
Essa ciência se correlaciona com todas as áreas do conhecimento e tem como função principal auxiliar o método científico em diversas fases, desde a coleta até a interpretação e a estimação de parâmetros populacionais.

Conceitos em estatística

A estatística é, de maneira geral, fundamental à análise e à interpretação de dados que apresentam variabilidade, bem como à elaboração de conclusões que servirão para tomada de decisão e para elaboração de ações em diferentes áreas do conhecimento. Podemos dividi-la em três áreas principais, conforme Figura 4.1.

• Estatística descritiva: tem por objetivo sintetizar e descrever uma série de dados de mesma natureza, permitindo uma visão geral sobre a variação desses valores.

  Exemplificando
  

  A estatística descritiva permite organizar e descrever os dados por meio de tabelas, gráficos e medidas descritivas. Por exemplo, descrever características sociodemográficas de uma população, como idade, sexo, etnia, altura, etc.

• Probabilidade: teoria matemática que estuda a incerteza proveniente de fenômenos de caráter aleatório. Ou seja, diz respeito à chance de que algo ocorra, como a chance de obter cara ou coroa no lançamento de uma moeda ou de que uma pessoa desenvolva determinada complicação ou doença em um contexto.
• Inferência estatística: ao contrário da estatística descritiva, ela faz afirmações sobre características de uma população por meio da análise de uma amostra. É amplamente utilizada em estudos epidemiológicos, pois torna viável investigações de grandes populações.

Além de estatística, é importante conceituar também o termo bioestatística, que nada mais é que a estatística aplicada a dados biológicos, seja de animais, seja de seres humanos ou de outros seres vivos.
Agora que já sabemos o que, de fato, é estatística e alguns de seus desdobramentos, faz-se imprescindível compreender alguns termos-chave utilizados para seu estudo.

• População: representa o conjunto de pessoas ou de coisas que têm uma característica observável comum. Por exemplo, moradores da região Nordeste do Brasil ou as árvores de determinada área. Podemos distinguir população ainda em dois tipos: populações comuns e populações estatísticas.
  As populações comuns contemplam a definição mais geral de “população”, citada acima, enquanto que populações estatísticas não se referem a pessoas ou a objetos de estudo, mas a características específicas desses elementos.
  
• Amostra: representa um subconjunto da população, ou seja, são elementos da população de interesse selecionados para determinada análise, já que estudar todos os componentes de uma população nem sempre é viável ou possível.
• Dados: são observações documentadas ou resultados de medições de características de interesse. Exemplo: os dados podem ser sobre a altura dos participantes e podem ser registrados em centímetros, por exemplo.
• Variável: é toda característica que pode diferir ou variar de membro para membro do estudo (os membros podem ser seres humanos, outros seres vivos ou objetos). Por exemplo: a variável peso, altura, etnia e renda são características que variam entre os componentes da amostra ou população. Explicitaremos a seguir os principais tipos de variáveis.

Tipos de variáveis

As variáveis são classificadas em dois grupos principais: as variáveis qualitativas e as quantitativas.
Variáveis qualitativas: são também conhecidas como categóricas e representam um atributo ou uma qualidade do participante da pesquisa. Apresentam-se em dois grupos:

• Nominal: para essas variáveis não existe uma ordenação por valores quantitativos, mas são definidas por categorias que classificam o indivíduo com determinada característica.
  Exemplos: sexo, etnia, orientação sexual, tipo sanguíneo, causa da morte, tipo de doença.
  
• Ordinal: nesses casos há ordenação ou diferentes graus nos possíveis resultados.
  Exemplos: classe social (A, B, C,...), grau de escolaridade (ensino básico, fundamental, superior, pós-graduação), intensidade de dor (nenhuma, leve, moderada, forte).
  

Variáveis quantitativas: apresentam valores que podem ser exprimidos por números. Dividem-se em dois grupos:

• Discreta: os possíveis valores se apresentam como um conjunto finito ou enumerável. Não estão relacionados a uma escala de medida específica.
  Exemplo: número de habitantes, número de filhos, número de células em uma cultura de laboratório.
  
• Contínua: assume valores que, frequentemente, formam um intervalo de números reais resultantes de uma mensuração.
  Exemplo: altura dos brasileiros (em centímetros), peso de idosos diabéticos (em quilogramas), valores de pressão arterial de um grupo (em milímetros de mercúrio – mmHg), distância entre dois países (em quilômetros).
  

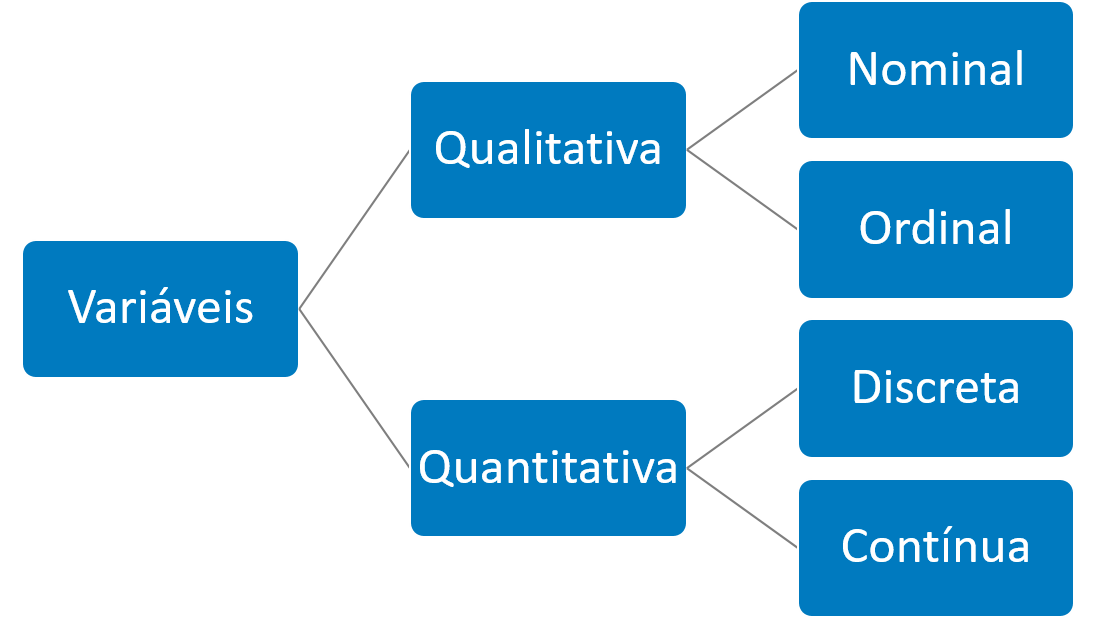
Tipos de escalas de medidas

Quando medimos alguma variável, automaticamente atribuímos a ela números, termos, letras ou símbolos que a caracterizam por meio de diferentes escalas. Por exemplo, utilizamos centímetros (cm) quando medimos a circunferência abdominal de indivíduos ou mililitros (ml) para determinarmos a quantidade de uma droga administrada.
As escalas se dividem em quatro tipos principais: nominal, ordinal, intervalar e proporcional (ou razão).

• Escala nominal: é o tipo mais básico entre as escalas e é meramente classificativa, sem nenhuma informação relacionada a valor ou à quantidade. A comparação, nesse caso, é feita entre o que é “semelhante” ou “divergente”. Além disso, não há como estabelecer o conceito de maior ou menor. Por exemplo: classificar em sexo masculino ou sexo feminino.
• Escala ordinal: também classificativa, como a nominal, porém, nesse caso, há como diferenciar o que é “menor”, o que é “menor” ou “crescente” e o que é “decrescente”, ou seja, há diferentes classes que se organizam em diferentes graus de acordo com critérios estabelecidos. Por exemplo: estadiamento do câncer de grau I a IV.
• Escala intervalar: é uma forma quantitativa de registrar a intensidade de determinado fenômeno medido. Utilizam-se os termos “quanto mais” e “quanto menos”. Para essas escalas determina-se um ponto zero arbitrário (não verdadeiro) e a aferição ocorre definindo-se a unidade de medida e comparando o “ponto zero” com um segundo valor conhecido. 
  É importante considerar que o ponto zero na escala não significa necessariamente ausência da característica. Por exemplo: a escala de temperatura é determinada em Celsius, na qual zero é o ponto de congelamento da água e 100 é o ponto de ebulição. No entanto, não podemos dizer que não há temperatura a zero graus, já que o zero nesse caso é também uma temperatura, que pode inclusive cair para valores negativos (-1, -2 graus). 
  
• Escala de proporcionalidade ou razões: é considerada a mais sofisticada entre as escalas, pois nela há um zero absoluto (verdadeiro), o qual é representado pela total ausência de uma característica ou de uma propriedade. Por exemplo: o peso de um corpo é um ponto de referência natural, em que zero representa, de fato, a ausência da característica peso, e o valor 2kg é, de fato, duas vezes maior do que o valor “1”, o que assegura as propriedades matemáticas e torna possível quantificar exatamente as diferenças entre as medições, ao contrário do exemplo da temperatura da água, no qual o zero havia sido estabelecido de maneira arbitrária (temperatura de congelamento da água).

Tipos de amostragem

É muito frequente que, em estudos de diversas áreas do conhecimento, seja inviável ou impossível acessar todos os indivíduos ou componentes de uma população. Por isso, como já descrito anteriormente nesta seção, seleciona-se uma porção dessa população, que é denominada amostra. Essa amostra deve ser suficiente para expressar as características de toda a população de interesse, logo podemos entender que o termo “amostragem” diz respeito ao ato de analisar uma pequena parte de um grande grupo a fim de aprender mais sobre esse grupo maior.
A Figura 4.3 lista os motivos que levam à utilização das técnicas de amostragem em estudos científicos.

Quanto ao tipo de amostragem, podemos dividir em dois tipos principais:

• Não probabilística: não se conhece a probabilidade de cada unidade amostral pertencer à amostra, cuja seleção depende do julgamento do pesquisador. Há três tipos de amostragem não probabilística:
  • Amostragem por conveniência: os participantes são selecionados pela facilidade de acesso a eles. É menos rigoroso se comparado aos demais métodos. Exemplo: um repórter entrevista pessoas que transitam na rua no momento.
  • Amostragem intencional: como o próprio nome já diz, a amostra é escolhida propositalmente, o que exige um conhecimento prévio do subgrupo selecionado e da característica que se quer analisar/observar.
  • Amostragem por cotas: é a que, dentre as amostragens não probabilísticas, possui maior rigor. Nesse método, inicialmente a população é classificada e, em seguida, determina-se a proporção entre as diferentes classes, e as cotas são fixadas tendo em vista a proporção delas. É utilizada em pesquisa eleitoral e de mercado.

É importante considerar que, nesse tipo de amostragem, não há igual probabilidade, entre os elementos da população, de que serão selecionados, logo não há garantia de representatividade da população.

• Probabilística: cada unidade amostral tem a mesma probabilidade de pertencer à amostra, sendo utilizada alguma forma de sorteio (aleatorização) para se determinar a amostra. Dividem-se em quatro tipos principais:
  • Amostragem aleatória simples: nesse processo, todos os elementos da população têm igual probabilidade de serem incluídos na amostra, sendo indicado para populações homogêneas, ou seja, com características semelhantes, sem grandes variações entre os elementos. Para tal, rotulam-se todos os componentes da população e um sorteio é realizado para saber quais farão parte da amostra.
  • Amostragem sistemática: ocorre quando os elementos da população estão dispostos de maneira organizada, como em filas, em listas, entre outras formas, e quando se tem um ponto de partida para selecionar, a cada número específico de integrantes, um elemento. Exemplo: em uma fábrica, a cada 100 seringas produzidas uma é retirada para inspeção de qualidade, compondo, assim, a amostra da população total de seringas produzidas.
  • Amostragem estratificada: nesse tipo de amostragem, divide-se a população em estratos (subgrupos) homogêneos, cujos critérios podem ser idade, sexo, renda, entre outras características. Quanto à forma de seleção da amostra, poderá ainda ser:
    • Uniforme: o mesmo número de participantes é sorteado entre os diferentes estratos.
    • Proporcional: nesse caso os estratos deverão ser proporcionais ao que existe na população.
    • Ótima: nesse caso o tamanho das camadas é definido em proporção ao desvio-padrão das variáveis estudadas, a fim de representar melhor a população.
  • Amostragem por conglomerados: a população é dividida em conglomerados ou clusters, sendo que, aleatoriamente, um conjunto de conglomerados é selecionado como representativo da população.

É imprescindível ressaltar a importância de selecionar os componentes que realmente expressem a característica que se quer estudar para a composição da amostra, além de assegurar que a amostra não é tendenciosa. Por exemplo, uma pesquisa que objetiva saber qual é o estilo musical favorito da população brasileira não pode ser realizada na fila de um show de rock, afinal a maioria esmagadora escolheria esse estilo musical como seu favorito, o que não necessariamente refletiria o gosto da população como um todo. Por fim, pode-se dizer que um dos principais cuidados com a amostra diz respeito a seu tamanho, que deve ser adequado. Para saber o tamanho amostral ideal, é preciso determinar o número mínimo de participantes por meio de cálculos específicos. Atualmente há diversos sites que disponibilizam gratuitamente ferramentas para calcular tamanho amostral. 
Agora que você já conhece os principais conceitos de estatística e de bioestatística, é importante correlacioná-los com o que foi apresentado no decorrer da disciplina de Saúde Pública. Conhecer as bases da bioestatística é fundamental para a prática profissional na área da saúde como um todo. Até a próxima seção!

Faça valer a pena

Referências

ALMEIDA FILHO, N. Epidemiologia sem números: introdução crítica à ciência epidemiológica. Rio de Janeiro: Editora Campus, 1989.

BARRETO, M. L. A. Epidemiologia, sua história e crises: notas para pensar o futuro. In: COSTA, D. C. Epidemiologia: teoria e objeto. São Paulo: Hucitec-Abrasco, 1990.

BUSSAB, W. O.; MORETTIN, P. A. Estatística básica. 9. ed. São Paulo: Saraiva, 2017. E-book. 

CALLEGARI-JAQUES, S. M. Bioestatística: princípios e aplicações. Porto Alegre: Artmed, 2007. E-book. 

MAGALHÃES, M. N.; LIMA, A. C.P. Noções de Probabilidade e Estatística. São Paulo: EDUSP, 2008.

STIGLER, S. M. The history of statistics: the measurement of uncertainty before 1900. Cambridge: Harvard University Press, 1986.

VIRGILLITO, S. B. Estatística aplicada. São Paulo: Saraiva, 2017. E-book.

ZWARCWALD, C. L.; CASTILHO, E. A. Os caminhos da estatística e suas incursões pela epidemiologia. Cad. Saúde Pública, Rio de Janeiro, v. 8, n. 1, p. 5-21, 1992. Disponível em: https://bit.ly/3cCrUOS. Acesso em: 4 jan. 2021.