Fonte: Shutterstock.
Áudio disponível no material digital.
Praticar para aprender
Prezados estudantes, daremos início agora à segunda seção desta unidade. Nela aprofundaremos nossos conhecimentos sobre as diferentes formas de se representar um conjunto de dados por meio das medidas de posição as quais permitem identificar um valor que melhor o representa.
Iniciaremos a seção abordando, de maneira mais aprofundada, a estatística descritiva, cujo principal objetivo é analisar as características dos dados da etapa inicial e que permite avançar para análises mais aprofundadas com outras abordagens estatísticas.
Trataremos também das medidas de posição: média, mediana e moda. As definições e cálculos serão apresentados de forma a explicitar a importância dessas medidas para melhor representação dos dados.
Outro ponto a ser abordado é o cálculo do desvio médio, que permite identificar a distância média que todos os elementos de um conjunto se encontram do ponto médio da série. Esse cálculo introduz as medidas de dispersão que serão tratadas na próxima seção da unidade.
Por fim, estudaremos os conceitos de frequência e encerraremos a seção tratando de gráficos e tabelas, desde suas principais características até seus tipos e sua pertinência frente ao tipo de variável.
Todos os temas serão apresentados com diversos exemplos e serão contextualizados para melhor compreensão e aplicação da estatística na prática profissional.
Considerando os conteúdos a serem apresentados nesta seção, vamos novamente acompanhar um grupo de pesquisadores que deseja realizar um estudo sobre a presença de doenças crônicas em trabalhadores da indústria têxtil de uma cidade do Sudeste do Brasil.
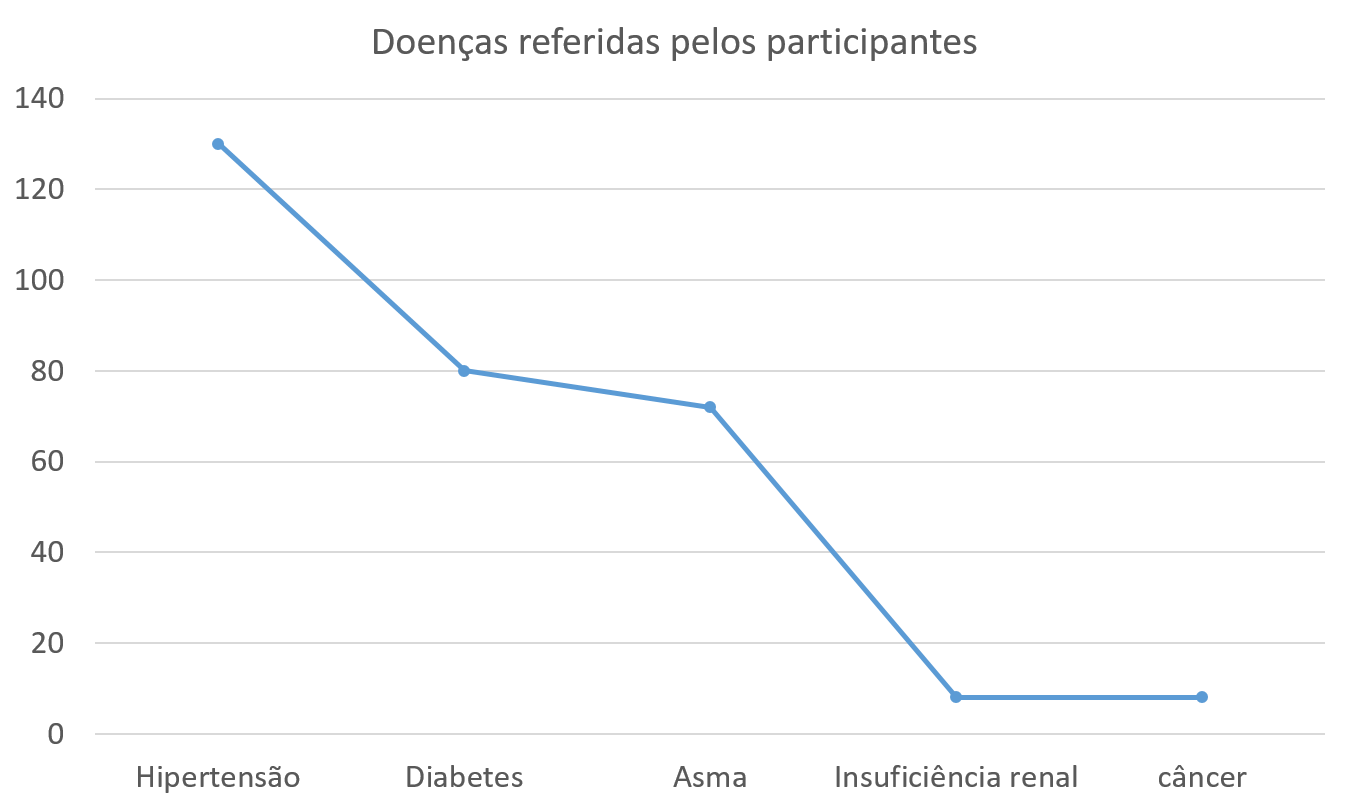
A essa altura, o grupo de pesquisadores já obteve a autorização do Comitê de Ética em Pesquisa, coletou todos os dados e agora está na fase de análise final e de construção dos resultados. Ao terminarem de escrever os resultados preliminares, os estudiosos decidem rever as tabelas e gráficos e se deparam com o gráfico a seguir.
Você, como membro integrante do grupo de pesquisa, como modificaria o gráfico acima? Qual a melhor maneira de se apresentar as informações das doenças referidas pelos participantes do estudo?
Bioestatística é uma ciência que está presente em várias outras ciências e presta uma contribuição imensurável para a sociedade. Conhecer suas bases fará com que seja um profissional de excelência e que, acima de tudo, faça a diferença por onde passe.
conceito-chave
Estatística descritiva
Ainda que com diferentes finalidades, a coleta de dados de natureza estatística ocorre em todas as áreas do conhecimento e atualmente está mais facilitada, sobretudo devido ao surgimento de diversos softwares para armazenamento e para análise de dados.
Observar extensos agrupamentos de dados com diversas características a serem analisadas não possibilita obter conclusões sensatas sobre nenhum assunto. Nesse sentido, uma análise que descreva inicialmente as características gerais é essencial.
A estatística descritiva é a análise inicial mais básica dos dados coletados. É a partir dessa técnica que é possível organizar, sintetizar, descrever ou mesmo comparar, entre os grupos, os principais aspectos dos dados coletados. Os resultados dessa análise descritiva podem ser apresentados em gráficos, tabelas, porcentagens, médias e índices.
A estatística descritiva vai muito além dos estudos científicos e está presente em muito do que consumimos socialmente, como em jornais, em revistas e em outras mídias sociais.
Exemplificando
Embora nem sempre percebamos, a estatística faz parte do nosso dia a dia. Por exemplo: ao ler alguma reportagem sobre a alta nos preços de alimentos, no ano de 2020, causada pela pandemia de Covid-19, é comum medirmos esse aumento em porcentagem, como no caso do arroz, que acumulou uma alta de 76% em seu valor durante o ano.
Outro exemplo ainda mais simples são as estatísticas de esportes, como o futebol, segundo as quais é possível ver o percentual de posse de bola entre os times durante a partida.
Medidas de posição
Como já vimos, a estatística descritiva otimiza a interpretação de um ou mais conjuntos de dados e permite uma análise mais completa das características observadas, seja por meio de números percentuais, seja por meio de gráficos, tabelas, etc. Entretanto, é possível resumi-los ainda mais e encontrar valores que representam uma série inteira de dados que se quer analisar. Esses valores ainda mais resumidos são capazes de caracterizar a tendência central dos dados e de sua dispersão.
As medidas de posição ou de tendência central mostram um valor representativo, ou seja, sintetizam os dados de um valor em torno do qual os dados do conjunto observável se distribuem.
Podemos dividir as medidas de posição em:
Média
A média aritmética nada mais é que a resultante da somatória de todos os elementos do conjunto dividida pela soma do número total de elementos.
Média =
Sendo , o símbolo que representa média.
Por exemplo: para saber a média aritmética da temperatura na última semana, deve-se somar as temperaturas de cada dia e dividir a soma pelo número de dias. Para fins didáticos, observe o Quadro 4.1 que apresenta os dados sobre a temperatura em cada um dos dias de uma semana.
| Dia | Temperatura |
|---|---|
| 1 | 27ºC |
| 2 | 28ºC |
| 3 | 30ºC |
| 4 | 29ºC |
| 5 | 25ºC |
| 6 | 23ºC |
| 7 | 17ºC |
Devemos então aplicar os valores do quadro na fórmula:
Média =
Logo, podemos concluir que a média de temperatura dessa semana foi de aproximadamente 25,6ºC.
Assimile
Há também a média ponderada, cuja principal diferença em relação à média aritmética é que aquela leva em consideração o peso de cada um dos termos, enquanto que nesta todos os termos possuem o mesmo peso.
Fórmula da média ponderada:
Média Ponderada =
Exemplo: em um cálculo da média ponderada das notas de uma prova, deve-se somar as multiplicações entre valores e pesos e dividir pela soma dos pesos.
O Quadro 4.2 apresenta os dados referentes à nota da prova e o número de alunos que atingiram cada um dos valores.
| Número de Alunos |
Notas |
|---|---|
| 4 | 10,0 |
| 2 | 8,5 |
| 3 | 6,0 |
| 3 | 5,0 |
Média Ponderada = = = = 7,5
Mediana
A mediana representa o “valor do meio” ou a posição central de um conjunto de dados. Para que que esse valor seja encontrado, os dados devem estar organizados em ordem crescente ou decrescente.
Em conjuntos com número ímpar de dados, a mediana será representada pelo valor que estiver ocupando o meio da série. Já em conjuntos com número par de dados, o valor da mediana corresponderá à média aritmética dos dois valores centrais.
Exemplo de conjunto de dados com número ímpar de componentes:
Em um conjunto de dados sobre a temperatura em treze dias diferentes, o valor da mediana será representado pelo número que se encontrar exatamente no meio do conjunto. Em nosso exemplo no Quadro 4.3, os dados já estão organizados em ordem crescente.
| Dia | Temperatura |
|---|---|
| 1 | 21ºC |
| 2 | 22ºC |
| 3 | 23ºC |
| 4 | 24ºC |
| 5 | 25ºC |
| 6 | 26ºC |
| 7 | 27ºC |
| 8 | 28ºC |
| 9 | 29ºC |
| 10 | 30ºC |
| 11 | 31ºC |
| 12 | 32ºC |
| 13 | 33ºC |
O conjunto de dados é (21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33).
O dado que ocupa exatamente a posição central do conjunto é 27. Logo, ele representa a mediana desse conjunto.
Para um conjunto com número par de elementos, devemos encontrar a média aritmética simples dos dois valores centrais.
Exemplo: conjunto de dados: (4; 8; 9; 12; 5; 7).
Inicialmente organizamos os dados em ordem: (4; 5; 7; 8; 9; 12).
Identificamos os dois valores centrais: (4; 5; 7; 8; 9; 12). Nesse caso, os valores 7 e 8 devem ser somados e divididos por dois. A mediana será (7 + 8) / 2 = 7,5.
Assimile
Passo a passo para encontrar a mediana em um conjunto de dados:
- Organize os dados em ordem crescente ou decrescente.
- Verifique se é um conjunto com número par ou ímpar de elementos.
- Caso seja um conjunto com número ímpar de elementos, a mediana será o seu valor central.
- Caso seja um conjunto com número par de elementos, deve-se fazer a média aritmética dos dois valores centrais e dividir a soma por dois para encontrar a mediana do conjunto.
Moda
A moda é representada pelo valor mais frequente em um conjunto de dados. Esse valor pode ser identificado observando-se a série de dados que se pretende analisar.
Exemplo:
Conjunto de dados: (2,3; 1,8; 4,5; 8; 12; 7; 1,8; 3,5; 1,8). Ao analisarmos o conjunto de dados, é possível observar que 1,8 é o elemento mais frequente, logo, para essa série de dados, há apenas uma moda (1,8). Esse conjunto de dados é, portanto, unimodal.
Quando existem duas modas, o conjunto será bimodal.
Exemplo: (2,3; 1,8; 4,5; 8; 12; 7; 1,8; 3,5; 2,3). Nesse caso há duas modas 2,3 e 1,8, e o conjunto é bimodal.
O conjunto pode ainda ser classificado como multimodal quando possuir mais de duas modas.
Exemplo: (2,3; 1,8; 3,5; 8; 12; 7; 1,8; 3,5; 2,3). As modas do conjunto são 2,3; 1;8 e 3,5, logo dizemos que ele é multimodal.
Há ainda a possibilidade de a série de dados não ter nenhum elemento que se repita, nesse caso diremos que é amodal.
Desvio médio
Pode ser definido como a média das distâncias dos valores do conjunto em relação à média.
Fórmula do desvio médio:
Os valores x1,x2,... xn representam cada um dos elementos do conjunto e, como já sabemos, representa a média. Por fim, “n” representa o número total de elementos. Logo, o desvio médio é igual (=) a cada um dos elementos do conjunto menos (-) a média aritmética do conjunto de dados em módulo somados, dividido pelo número total de elementos do conjunto.
É importante considerar, ainda, que os elementos devem ser calculados em módulo ou valor absoluto de um número real, que representa a distância desse número em relação à origem, já que o objetivo, nesse caso, é conhecer a distância em que cada elemento do conjunto se encontra da média. Portanto, o cálculo em módulo desconsidera o sinal, por exemplo, - 3 e + 3 estão à mesma distância do número zero, de modo que essa distância será sempre positiva.
Para melhor compreensão, vejamos o exemplo a seguir:
Levemos em consideração o seguinte conjunto: (-7; 4; 0; 3; 8; 10).
Para reconhecermos os valores na fórmula, notamos que x1 é igual ao primeiro elemento do conjunto (-7) e assim sucessivamente. Como “n” representa a quantidade de elementos no conjunto, nesse caso temos seis elementos.
Para a resolução do problema, seguimos o seguinte passo a passo:
1º passo: encontrar a média do conjunto. Para isso, é necessário somar todos os elementos e dividir a soma pelo número total de elementos do conjunto.
Logo, a média é igual a 3.
2º passo: aplicar os valores à fórmula.
Desvio Médio (Dam) = =
3º passo: calcular o desvio médio.
Desvio Médio (Dam) = =
Como os números estão em módulos, os negativos ficarão positivos.
Desvio Médio (Dam) = = = 4,33
Logo, podemos dizer que o desvio médio para essa série de dados é 4,33.
Distribuição de frequências, gráficos e tabelas
- Frequência absoluta: é o número de vezes que um evento ocorre em uma série de dados, ou seja, é a frequência com que determinado dado aparece num conjunto.
- Frequência relativa: é o quociente entre a frequência absoluta e o tamanho da amostra.
- Frequência percentual: é resultante da multiplicação da frequência relativa por 100.
- Frequência acumulada: é o total acumulado da soma de todas as classes anteriores até a classe atual.
Exemplificando
Em um conjunto de dados:
(8; 10; 15; 18; 15; 20; 22; 12; 11; 9; 15; 100; 13; 3; 1; 82; 87; 99)
- A frequência absoluta do elemento “15” será 3, pois ele ocorre três vezes no conjunto.
- A frequência relativa do elemento “15” poderá ser calculada tomando-se como base a frequência absoluta (nesse caso 3), dividida pelo número total de observações do conjunto (= 18 elementos). 3/18 = 0,17.
- A frequência percentual deverá ser calculada a partir da frequência relativa (0,17) multiplicada por 100, o que, nesse caso, seria 17%.
Para que os dados sejam melhor representados utilizamos instrumentos como tabelas e gráficos.
As tabelas têm por objetivo apresentar dados agrupados a fim de simplificar sua compreensão. Recomenda-se que a tabela:
- Tenha descrições suficientes a fim de que não haja necessidade de consulta ao texto para sua compreensão.
- Esteja disposta de forma simples e objetiva, contendo somente os dados necessários.
- Apresente ordenação lógica dos dados.
Os gráficos são também representações ilustrativas que servem para organizar e apresentar, de maneira mais clara e objetiva, os dados. Deve ser composto por título, subtítulo, fonte e eixos vertical (y) e horizontal (x), que podem ser visíveis ou não.
Como já estudamos na seção anterior, os dados podem ser de diferentes naturezas (quantitativos e qualitativos) e, dessa forma, é necessário estudar as principais ferramentas utilizadas para melhor organizá-los e apresentá-los. Veja a seguir a partir de gráficos e tabelas.
Exemplo de tabela:
Com o intuito de verificar a variável sexo numa população de 97 estudantes, seria mais viável apresentar as categorias masculino e feminino numa linha, conforme mostra a Tabela 4.1.
| Sexo | Frequência absoluta | Frequência relativa (%) |
|---|---|---|
| Feminino | 35 | 36,1 |
| Masculino | 62 | 63,9 |
| Total | 97 | 100 |
Utilizando ainda o mesmo exemplo da variável “sexo”, a informação da tabela pode também ser representada em gráfico. Apresentaremos dois exemplos de gráficos para a apresentação de variáveis qualitativas: o gráfico setorial, popularmente conhecido como “pizza”, e o gráfico de coluna.
Gráficos setoriais: são utilizados para mostrar a importância relativa das proporções. Geralmente usam porcentagens.
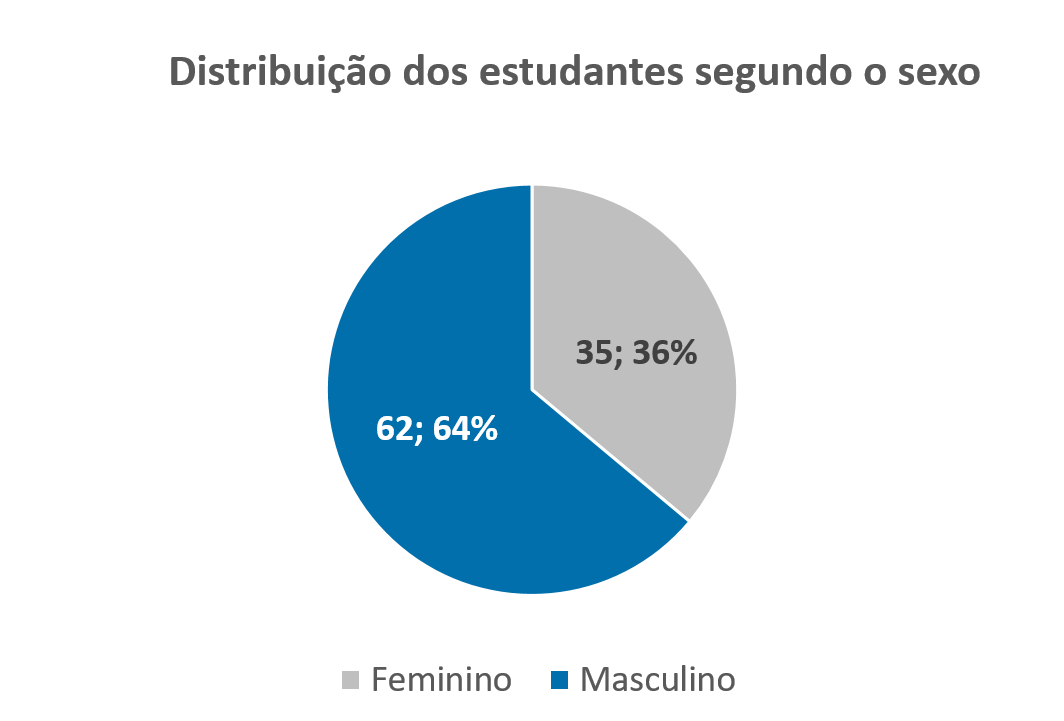
Gráficos de coluna: podem ilustrar comparações entre itens ou até demonstrar alterações de dados em determinado período.
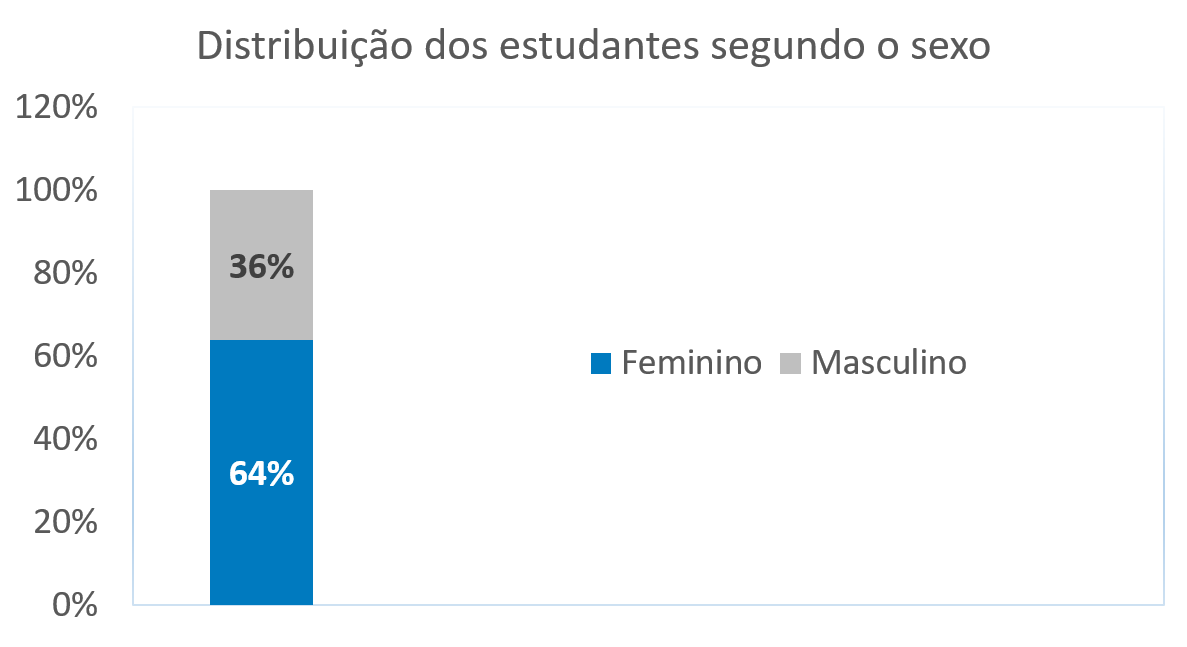
Gráficos em linha: representam observações feitas ao longo de um período e demonstram o comportamento de determinado fenômeno e suas tendências. Temos como exemplo o gráfico a seguir do Ministério da Saúde (Figura 4.7).
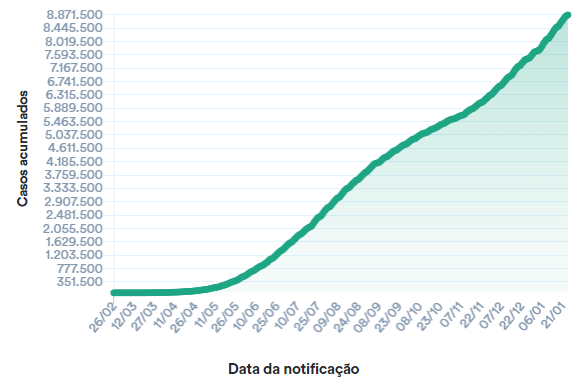
Há ainda os histogramas, que são um conjunto de retângulos com bases sobre um eixo horizontal, divididos de acordo com o tamanho das classes polígono de frequências, polígonos de frequências acumuladas percentuais, entre outros.
Reflita
É imprescindível compreender as bases e os conceitos iniciais da estatística, pois conhecer os dados e os tipos de variáveis analisadas possibilita escolher o tipo mais adequado de apresentação, seja por tabelas ou diferentes gráficos, seja pela apresentação da informação de maneira descritiva. Dentro do contexto da saúde pública, por quais motivos essas ferramentas denotam tal importância?
Chegamos ao fim de mais uma seção e agora você já conhece algumas formas possíveis de sintetizar séries de dados para melhor apresentá-los e interpretá-los. Isso é essencial em qualquer pesquisa e faz parte do cotidiano de muitos profissionais da área da saúde. Por isso, é imprescindível que tente aplicar esses conhecimentos, tendo como base todo conteúdo já visto até aqui.
Faça valer a pena
Questão 1
A estatística descritiva permite otimizar a interpretação de um conjunto de dados e analisar, com maior precisão, suas características. É possível resumir ainda mais esses dados e encontrar um valor que represente a série inteira deles. Para isso servem as medidas de posição ou de tendência central.
Com relação às medidas de posição, assinale a alternativa correta:
Tente novamente...
INCORRETA, pois essa é a definição de moda.
Tente novamente...
INCORRETA, pois essa é a definição de média aritmética.
Correto!
CORRETA, pois, para se calcular a mediana de uma série de dados com número par, é necessário utilizar os dois valores centrais a fim de obter o número real, diferente de conjuntos com número ímpar, nos quais o elemento central é considerado a mediana.
Tente novamente...
INCORRETA, pois moda é representada pelo valor ou pelos valores que mais se repetem num conjunto de dados.
Tente novamente...
INCORRETA, pois em conjuntos de dados com número ímpar de elementos, basta apenas identificar o valor central.
Questão 2
Dentre as medidas de dispersão, o desvio médio pode ser definido como a média das distâncias dos valores do conjunto em relação à média. Seu cálculo é baseado em uma fórmula que leva em consideração variáveis como a média aritmética do conjunto e o número de elementos nele existentes.
Com relação ao cálculo de desvio médio, é correto afirmar que:
Tente novamente...
INCORRETA, pois deve-se subtrair da média e não somar.
Tente novamente...
INCORRETA, pois os elementos devem ser calculados em módulo.
Correto!
CORRETA, pois a média é parte da fórmula e, portanto, precisa ser calculada previamente.
Tente novamente...
INCORRETA, pois a finalidade é calcular a média de distância dos elementos em relação à média do conjunto.
Tente novamente...
INCORRETA, pois é necessário calcular apenas a média aritmética.
Questão 3
Para que os dados sejam mais bem representados e sintetizados, instrumentos como tabelas e gráficos são utilizados. Essas ferramentas têm por objetivo apresentar dados agrupados e simplificar sua compreensão.
Com relação aos gráficos e tabelas, é correto afirmar que:
Tente novamente...
INCORRETA, pois esses são os componentes do gráfico.
Correto!
CORRETA, pois é um instrumento que deve sintetizar e facilitar a análise de uma série de dados.
Tente novamente...
INCORRETA, pois devem conter apenas informações essenciais, de forma resumida.
Tente novamente...
INCORRETA, pois essa é a definição do gráfico em linha.
Tente novamente...
INCORRETA, pois essa é a definição do gráfico em colunas.
Referências
BUSSAB, W. O.; MORETTIN, P. A. Estatística básica. 9. ed. São Paulo: Saraiva, 2017. E-book.
CALLEGARI-JAQUES, S. M. Bioestatística: princípios e aplicações. Porto Alegre: Artmed, 2007. E-book.
CARVALHO, S.; CAMPOS, W. Estatística básica simplificada. Rio de Janeiro: Juspodivm, 2016.
COVID-SAÚDE. Painel Coronavírus. Coronavírus Brasil, Brasília, 2021. Disponível em: https://bit.ly/3czvKbx. Acesso em: 26 jan. 2021.
FEIJOO, A. M. L. C. de. Medidas de tendência central. In: FEIJOO, A. M. L. C. de. A pesquisa e a estatística na psicologia e na educação. Rio de Janeiro: Centro Edelstein de Pesquisas Sociais, 2010. p. 14-22. Disponível em: https://bit.ly/2RLTmSV. Acesso em: 10 jan. 2021.
FINKELMAN, J. Caminhos da saúde no Brasil. Rio de Janeiro: Editora FIOCRUZ, 2002. Disponível em: https://bit.ly/3iAwKQn. Acesso em: 13 maio 2021.
MAGALHÃES, M. N.; LIMA, A. C. P. de. Noções de Probabilidade e Estatística. São Paulo: EDUSP, 2008.
REIS, E. A., REIS I. A. Análise Descritiva de Dados. Relatório Técnico do Departamento de Estatística da UFMG. Belo Horizonte: UFMG, 2002. Disponível em: https://bit.ly/35aXcYP. Acesso em: 10 jan. 2021.