Analisando os comandos dos mecanismos de buscas
Vamos descobrir como se comportam os algoritmos de busca.

Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
INTRODUÇÃO
Você já fez alguma pesquisa no Google hoje? Já fez a busca por alguma passagem de avião, de ônibus, ou até mesmo a aquisição de algum item em um site de compras? Já procurou alguém nas redes sociais? Se tivermos o cadastro de clientes em uma loja, como faremos a busca por esses cliente? Podemos ter o cadastro de uma lista de RG e CPF para realizar essa busca.
Enfim, todas essas aplicações utilizam mecanismos de busca. Um grande diferencial entre uma ferramenta e outra é a velocidade da resposta: quanto mais rápido ela for, mais eficiente e melhor será a aceitação dela. Por trás de qualquer tipo de pesquisa existe um algoritmo de busca sendo executado. Nesta aula vamos aprender dois deles.
Algoritmos de buscas
"Os algoritmos são o cerne da computação" (TOSCANI; VELOSO, 2012, p. 1).
Com essa afirmação, iniciamos nossa aula, na qual estudaremos algoritmos de busca. Os algoritmos computacionais são desenvolvidos e usados para resolver os mais diversos problemas. Nesse universo, como o nome sugere, os algoritmos resolvem problemas relacionados ao encontro de valores em uma estrutura de dados.
Diversas são as aplicações que utilizam esse mecanismo.
Já nos deparamos, como usuários, com um algoritmo de busca nesta disciplina quando estudamos as estruturas de dados. Em Python, temos a operação "in" ou "not in" usada para verificar se um valor está em uma sequência. Quando utilizamos esses comandos, estamos sendo "usuários" de um algoritmo que alguém escreveu e "encapsulou" neles. No entanto, como profissionais de tecnologia, precisamos saber o que está por trás do comando. Observe o exemplo:
nomes = 'João Marcela Sonia Daryl Vernon Eder Mechelle Edan Igor Ethan Reed Travis Hoyt'.split()
print('Marcela' in nomes)
print('Roberto' in nomes)
Na entrada 1 (In [1]), usamos o operador in para verificar se dois nomes constavam na lista. No primeiro, obtivemos True; e no segundo, False. O que, no entanto, há "por trás" desse comando in? Que algoritmo foi implementado nesse operador? Um profissional de tecnologia, além de saber implementar, precisa conhecer o funcionamento dos algoritmos.
Busca linear (ou Busca Sequencial)
Como o nome sugere, uma busca linear (ou exaustiva) simplesmente percorre os elementos da sequência procurando aquele de destino, conforme ilustra a Figura 2.1.
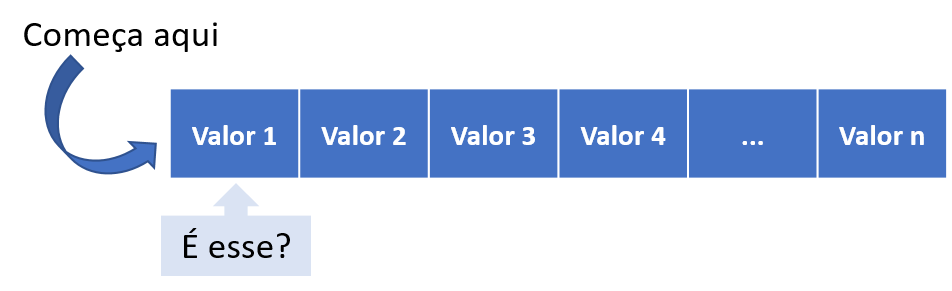
Veja que a busca começa por uma das extremidades da sequência e vai percorrendo até encontrar (ou não) o valor desejado. Com essa imagem, fica claro que uma pesquisa linear examina todos os elementos da sequência até encontrar o de destino, o que pode ser muito custoso computacionalmente, conforme veremos adiante.
Para implementar a busca linear, vamos precisar de uma estrutura de repetição (for) para percorrer a sequência, e uma estrutura de decisão (if) para verificar se o valor em uma determinada posição é o que procuramos. Vejamos como fazer a implementação em Python.
def executar_busca_linear(lista, valor):
for elemento in lista:
if valor == elemento:
return True
return False
import random
lista = random.sample(range(1000), 50)
print(sorted(lista))
executar_busca_linear(lista, 10)
Na entrada 2 (In [2]) criamos a função "executar_busca_linear", que recebe uma lista e um valor a ser localizado. Na linha 2, criamos a estrutura de repetição, que percorrerá cada elemento da lista pela comparação com o valor buscado (linha 3). Caso este seja localizado, então a função retorna o valor booleano True; caso não seja encontrado, então retorna False.
Para testarmos a função, criamos o código na entrada 3 (In[3]), no qual, por meio da biblioteca random (não se preocupe com a implementação, já que ainda veremos o uso de bibliotecas), criamos uma lista de 50 valores com números inteiros randômicos que variam entre 0 e 1000; e na linha 5 invocamos a função, passando a lista e um valor a ser localizado. Cada execução desse código gerará uma lista diferente, e o resultado poderá alterar.
Nossa função é capaz de determinar se um valor está ou não presente em uma sequência, certo? E se, no entanto, quiséssemos também saber sua posição na sequência? Em Python, as estruturas de dados do tipo sequência possuem a função index(), que é usada da seguinte forma: sequencia.index(valor). A função index() espera como parâmetro o valor a ser procurado na sequência. Observe o código a seguir.
vogais = 'aeiou'
resultado = vogais.index('e')
print(resultado)
Será que conseguimos implementar nossa própria versão de busca por index com utilização da busca linear? A resposta é sim! Podemos iterar sobre a lista e, quando o elemento for encontrado, retornar seu índice. Caso não seja encontrado, então a função deve retornar None. Vale ressaltar a importância dos tipos de valores que serão usados para realizar a busca. Dada uma lista numérica, somente podem ser localizados valores do mesmo tipo. O mesmo para uma sequência de caracteres, que só pode localizar letras, palavras ou ainda uma string vazia. O tipo None não pode ser localizado em nenhuma lista – se tentar passar como parâmetro, poderá receber um erro. Observe a função "procurar_valor" a seguir.
def procurar_valor(lista, valor):
tamanho_lista = len(lista)
for i in range(tamanho_lista):
if valor == lista[i]:
return i
return None
vogais = 'aeiou'
resultado = procurar_valor(lista=vogais, valor='a')
if resultado != None:
print(f"Valor encontrado na posição {resultado}")
else:
print("Valor não encontrado")
Na entrada 5 (In [5]), criamos a função "procurar_valor", a fim de retornar a posição de um valor, caso ele seja encontrado. Na entrada 6 (In [6]), criamos uma lista com as vogais e invocamos a função "procurar_valor", passando a lista e um valor a ser procurado. Na linha 5, testamos se existe valor na variável "resultado", já que, caso o valor guardado em "resultado" for None, então o else é acionado.
Vamos testar o código, agora, buscando o valor "o" na lista de vogais. Observe que a lista tem tamanho 5 (número de vogais), sendo representada com os índices 0 a 4. O valor foi alterado para a vogal "o" na linha 19 do código. Teste o código utilizando a ferramenta Python Tutor.
Observe que o valor "o" foi encontrado na posição 3 da lista. Nesse contexto, foi necessário percorrer os índices 0, 1, 2 e 3 até chegar à vogal procurada. Assim funciona a busca linear (sequencial): todas as posições são visitadas até que se encontre o elemento buscado. Caso a busca fosse por um valor que não está na lista, o valor retornado seria None.
Acabamos de implementar nossa versão da função index. Será que ela é melhor que a função index() das sequências em Python? Se tentarmos executar a função index(), passando como parâmetro um valor que não está na lista, teremos um erro como resultado: "ValueError". Por sua vez, na nossa versão, caso o valor não esteja na lista, não será retornado um erro, mas simplesmente o valor None. Você pode utilizar o emulador para fazer novos testes e aprimorar seus estudos!
Precisamos falar sobre complexidade
Nossa função procurar_valor tem um comportamento diferente da função index() para os valores não encontrados. Será que isso é uma característica que pode ser levada em consideração para determinar que um algoritmo é melhor que o outro? A resposta é não!
Em termos computacionais, um algoritmo é considerado melhor que o outro quando, para a mesma entrada, utiliza menos recursos computacionais em termos de memória e processamento. Um exemplo clássico é a comparação entre os métodos de Cramer e Gauss, usados para resolver equações lineares. O método de Cramer pode levar dezenas de milhões de anos para resolver um sistema matricial de 20 linhas por 20 colunas, ao passo que o método de Gauss pode levar alguns segundos (TOSCANI; VELOSO, 2012). Veja a diferença: para a mesma entrada há um algoritmo que é inviável! Esse estudo da viabilidade de um algoritmo, em termos de espaço e tempo de processamento, é chamado de análise da complexidade do algoritmo.
Para começarmos a compreender intuitivamente, pense na lista de alunos, em ordem alfabética, de toda a rede Kroton/Cogna: estamos falando de cerca de 1,5 milhões de alunos. Dada a necessidade de encontrar um aluno, você acha mais eficiente procurá-lo pela lista inteira, um por um, ou dividir essa lista ao meio e verificar se o nome buscado está na parte superior ou inferior?
A análise da complexidade do algoritmo fornece mecanismos para medir o desempenho de um algoritmo em termos de "tamanho do problema versus tempo de execução" (TOSCANI; VELOSO, 2012). A análise da complexidade é feita em duas dimensões: espaço e tempo. Embora ambas as dimensões influenciem na eficiência de um algoritmo, o tempo que ele leva para executar é tido como a característica mais relevante, pois, como vimos na comparação com os métodos de Cramer e Gauss, o primeiro é impossível de ser utilizado.
Essa análise tem de ser feita sem considerar o hardware, pois sabemos que uma solução executada em um processador mais potente certamente levará menos tempo de execução do que se ocorrer em um menos potente. Não é esse tipo de medida que a análise da complexidade está interessada em estudar: o que interessa saber é qual função matemática expressa o comportamento do tempo, principalmente, para grandes entradas de dados. Por exemplo, no caso de nossa função "executar_busca_linear", conforme o tamanho da lista aumenta, o tempo necessário para achar um valor pode aumentar, principalmente se este estiver nas posições finais da lista.
Essa reflexão sobre a posição do valor na lista nos leva a outros conceitos da análise da complexidade: a medida do tempo com relação ao melhor caso, ao pior caso e ao caso médio. Usando a busca linear, se o valor procurado estiver nas primeiras posições, temos o melhor cenário de tempo, independentemente do tamanho da lista, uma vez que, assim que o valor for localizado, a execução da função já se encerra. Se o valor estiver no meio da lista, temos um cenário mediano de complexidade, pois o tamanho da lista começa a ter influência no tempo da busca. Se o valor estiver no final da lista, teremos o pior caso, já que o tamanho da lista influenciará totalmente o tempo de execução.
A análise da complexidade está interessa em medir o desempenho de um algoritmo para grandes entradas, ou seja, para o pior caso (TOSCANI; VELOSO, 2012). Podemos, então, concluir que a análise da complexidade de um algoritmo tem como um dos grandes objetivos encontrar o comportamento do algoritmo (a função matemática) em relação ao tempo de execução para o pior caso, ao que chamamos de complexidade assintótica. "A complexidade assintótica é definida pelo crescimento da complexidade para entradas suficientemente grandes. O comportamento assintótico de um algoritmo é o mais procurado, já que, para um volume grande de dados, a complexidade torna-se mais importante. O algoritmo assintoticamente mais eficiente é melhor para todas as entradas, exceto talvez para entradas relativamente pequenas." (TOSCANI; VELOSO, 2012, p. 24).
A complexidade é expressa por uma função matemática f(n), em que n é o tamanho da entrada. Para determinar a complexidade, a função é dividida em um termo dominante e termos de ordem inferior, pois estes últimos e as contantes são excluídos. Por exemplo, vamos supor que a função f(n) = an2 + bn + c (função do segundo grau) é a função de tempo de um determinado algoritmo. Para expressar sua complexidade, identifica-se qual é o termo dominante (nesse caso, o parâmetro com maior crescimento é n2). Ignoram-se os termos de ordem inferior (nesse caso n) e ignoram-se as constantes (a, b, c), razão pela qual ficamos, então, com a função f(n) = n2. Portanto, a função de complexidade para esse algoritmo é denotada pela notação assintótica O(n2), chamada de Big-Oh (Grande-O).
Toda essa simplificação é embasada em conceitos matemáticos (limites) que não fazem parte do escopo desta disciplina. A análise assintótica é um método usado para descrever o comportamento de limites, razão pela qual é adotada pela análise da complexidade. Para saber mais profundamente sobre essa importante área da computação, recomendamos a leitura de: CORMEN et al. Introduction to Algorithms. Cambridge: The MIT Press, 2001.
EXEMPLIFICANDO
Agora que já conhecemos os conceitos básicos da análise da complexidade de algoritmos, vamos fazer a análise do algoritmo de busca sequencial, considerando nossa função procurar_valor. A Figura 2.2 ilustra a análise que queremos fazer.
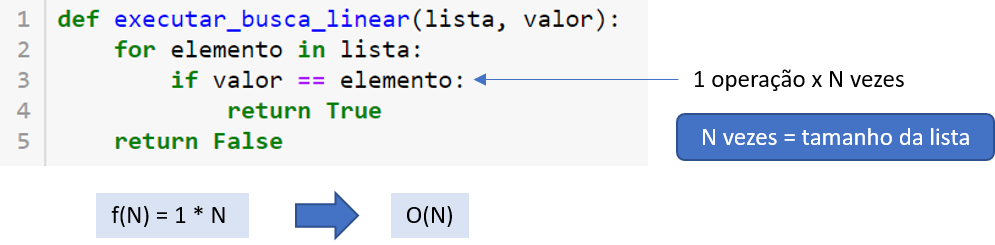
Para isso, vamos considerar as operações em alto nível, ou seja, não vamos nos preocupar com as operações no nível de máquina. Por exemplo, na linha 4 temos uma operação de alto nível, que será executada N vezes (sendo N o tamanho da lista). Portanto, a função que determina o tempo de execução é f(N) = 1 * N. Porém, queremos representar a complexidade assintótica usando a notação Big-Oh, razão pela qual, ao excluirmos os termos de menor ordem e as constantes da equação, obtemos O(N) como a complexidade do algoritmo de busca linear (STEPHENS, 2013).
A notação O(N) representa uma complexidade linear. Ou seja, o tempo de execução aumentará de forma linear com o tamanho da entrada. Outras complexidades que são comumente encontradas são: O(log N), O(N2), O(N3). Vale ressaltar que, em termos de eficiência, teremos que: O(1) < O(log N) < O(N) < O(N2) < O(N3) < O(2N), ou seja, um algoritmo com complexidade O(N) é mais eficiente que O(N2).
Busca binária
Outro algoritmo usado para buscar um valor em uma sequência é o de busca binária. A primeira grande diferença entre o algoritmo de busca linear e o algoritmo de busca binária é que, com este último, os valores precisam estar ordenados. A lógica é a seguinte:
- Encontra o item no meio da sequência (meio da lista).
- Se o valor procurado for igual ao item do meio, a busca se encerra.
- Se não for, verifica-se se o valor buscado é maior ou menor que o valor central.
- Se for maior, então a busca acontecerá na metade superior da sequência (a inferior é descartada); se não for, a busca acontecerá na metada inferior da sequência (a superior é descartada).
Veja que o algoritmo, ao encontrar o valor central de uma sequência, a divide em duas partes, o que justifica o nome de busca binária. A Figura 2.3 ilustra o funcionamento do algoritmo na busca pelo número 14 em uma certa sequência numérica.
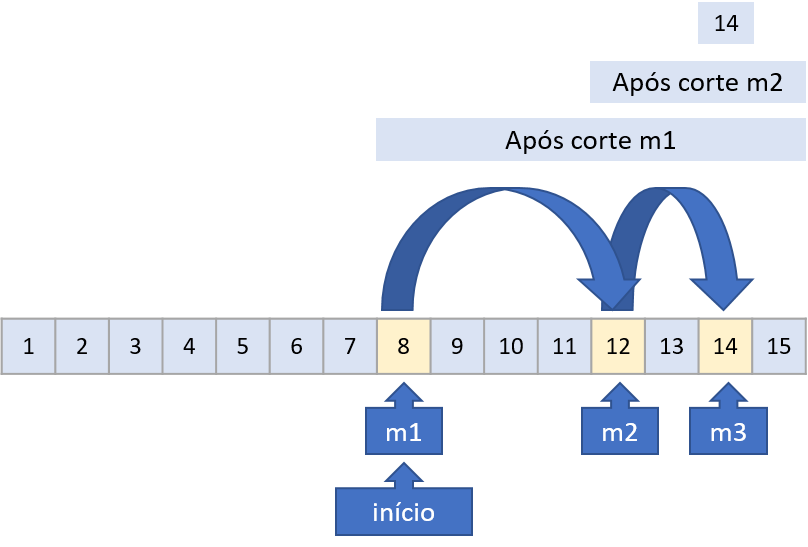
Veja que o algoritmo começa encontrando o valor central, ao qual damos o nome de m1. Como o valor buscado não é o central, sendo maior que ele, então a busca passa a acontecer na metade superior. Dado o novo conjunto, novamente é localizado o valor central, o qual chamamos de m2, que também é diferente do valor buscado, sendo menor que este. Mais uma vez a metade superior é considerada e, ao localizar o valor central, agora sim trata-se do valor procurado, razão pela qual o algoritmo encerra. Veja que usamos retângulos para representar os conjuntos de dados após serem feitos os testes com os valores centrais. Como pode ser observado, cada vez mais o conjunto a ser procurado diminui.
Os retângulos usados na Figura 2.3 para ilustrar o conjunto de dados após encontrar o meio, checar se o valor é maior ou menor e excluir uma parte demonstram a seguinte situação:
Suponha que tenhamos uma lista com 1024 elementos. Na primeira iteração do loop, ao encontrar o meio e excluir uma parte, a lista a ser buscada já é diminuída para 512. Na segunda iteração, novamente ao encontrar o meio e excluir uma parte, restam 256 elementos. Na terceira iteração, restam 128. Na quarta, restam 64. Na quinta, restam 32. Na sexta, restam 16. Na sétima 8. Na oitava 4. Na nona 2. Na décima iteração resta apenas 1 elemento. Ou seja, para 1024 elementos, no pior caso, o loop será executado apenas 10 vezes, diferentemente da busca linear, na qual a iteração aconteceria 1024 vezes.
A busca binária possui complexidade O(log2 N) (STEPHENS, 2013). Isso significa que, para valores grandes de N (listas grandes), o desempenho desse algoritmo é melhor se comparado à busca sequencial, que tem complexidade O(N). Para ficar claro o que isso significa, observe a Figura 2.4.
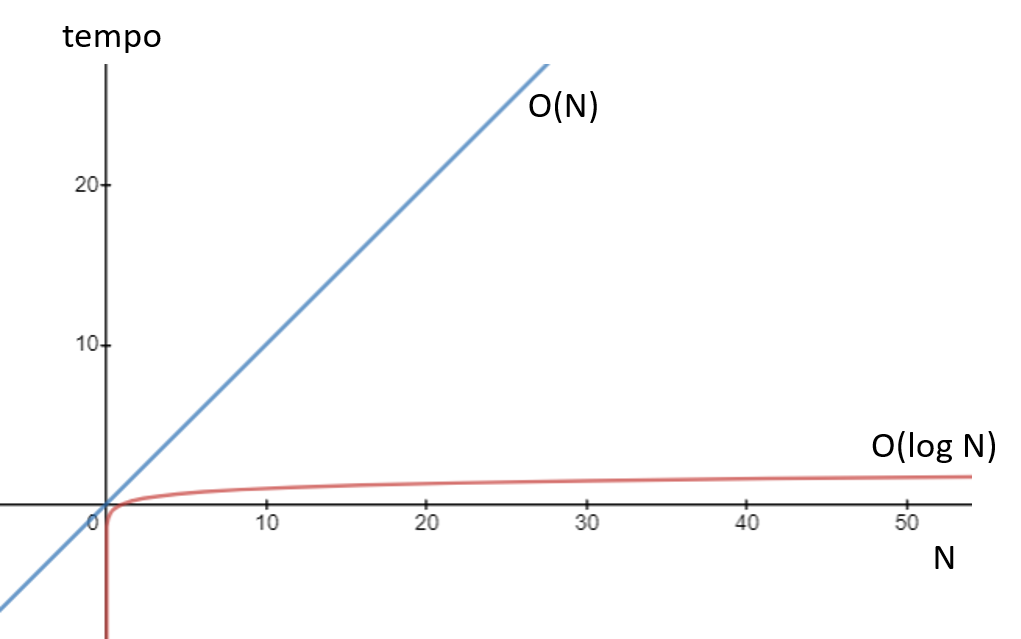
Nela construímos um gráfico com a função f(N) = N, que representa o comportamento da complexidade O(N), e outro gráfico com a função f(N) = log N, que representa, por sua vez, O(log N). Veja como o tempo da complexidade O(N) cresce muito mais rápido que O(log N), quando N aumenta.
Em Stephens (2013, p. 219), podemos encontrar o seguinte pseudocódigo para a busca binária:
Integer: BinarySearch(Data values[], Data target)
Integer: min = 0
Integer: max = - 1
While (min <= max)
// Find the dividing item.
Integer: mid = (min + max) / 2
// See if we need to search the left or right half.
If (target < values[mid]) Then max = mid - 1
Else If (target > values[mid]) Then min = mid + 1
Else Return mid
End While
// If we get here, the target is not in the array.
Return -1
End BinarySearch
Pois bem, agora que já conhecemos o algoritmo, basta escolhermos uma linguagem de programação e implementarmos. Veja como fica a busca binária em Python.
def executar_busca_binaria(lista, valor):
minimo = 0
maximo = len(lista) - 1
while minimo <= maximo:
# Encontra o elemento que divide a lista ao meio
meio = (minimo + maximo) // 2
# Verifica se o valor procurado está a esquerda ou direita do valor central
if valor < lista[meio]:
maximo = meio - 1
elif valor > lista[meio]:
minimo = meio + 1
else:
return True # Se o valor for encontrado para aqui
return False # Se chegar até aqui, significa que o valor não foi encontrado
lista = list(range(1, 50))
print(lista)
print('\n',executar_busca_binaria(lista=lista, valor=10))
print('\n', executar_busca_binaria(lista=lista, valor=200))
Na entrada 7 (In [7]), implementamos o algoritmo da busca binária.
Nas linhas 2 e 3, inicializamos as variáveis que contêm o primeiro e o último indíce da lista. No começo da execução, esses valores são o índice 0 para o mínimo e o último índice, que é o tamanho da lista menos 1. Essas variáveis serão atualizadas dentro do loop, conforme condição.
- Na linha 4 usamos o while como estrutura de repetição, pois não sabemos quantas vezes a repetição deverá ser executada. Esse while fará com que a execução seja feita para todos os casos binários.
- Na linha 6, usamos uma equação matemática (a média estatística) para encontrar o meio da lista.
- Na linha 8, checamos se o valor que estamos buscando é menor que o valor encontrado no meio da lista.
- Caso seja, então vamos para a linha 9, na qual atualizamos o índice máximo. Nesse cenário, vamos excluir a metade superior da lista original.
- Caso o valor não seja menor que o meio da lista, então vamos para a linha 10, na qual testamos se ele é maior. Se for, então atualizamos o menor índice, excluindo assim a metade inferior.
- Se o valor procurando não for nem menor nem maior e ainda estivermos dentro do loop, então ele é igual, e o valor True é retornado pelo comando na linha 13.
- Porém, se já fizemos todos os testes e não encontramos o valor, então é retornado False na linha 14.
Na entrada 8 (In [8]), testamos a função executar_busca_binaria. Veja que usamos a função range() para criar uma lista numérica de 50 valores ordenados. Nas linhas 5 e 6 testamos a função, procurando um valor que sabemos que existe e outro que não existe.
Como podemos alterar nossa função para que, en vez de retornar True ou False, retorne a posição que o valor ocupa da sequência? A lógica é a mesma. No entanto, agora vamos retornar a variável "meio", já que esta, se o valor for encontrado, será a posição. Observe o código a seguir.
def procurar_valor(lista, valor):
minimo = 0
maximo = len(lista) - 1
while minimo <= maximo:
meio = (minimo + maximo) // 2
if valor < lista[meio]:
maximo = meio - 1
elif valor > lista[meio]:
minimo = meio + 1
else:
return meio
return None
vogais = ['a', 'e', 'i', 'o', 'u']
resultado = procurar_valor(lista=vogais, valor='z')
if resultado:
print(f"Valor encontrado an posição {resultado}")
else:
print("Valor não encontrado")
Na entrada 9 (In [9]), alteramos a função executar_busca_binaria para procurar_valor. Esta função fará a busca com o uso do algoritmo binário. Veja que, nas linhas 11 e 12, alteramos o retorno da função. Na entrada 10, testamos o funcionamento do algoritmo.
Vamos buscar a vogal "o" utilizando o algoritmo de busca binária. Teste o código utilizando a ferramenta Python tutor.
Observe que é verificado se o valor procurado é igual ao valor da posição do meio da lista. Se o valor procurado é menor, o processo se repete considerando que a lista possui a metade do tamanho, razão pela qual inicia na posição seguinte do meio. Todavia, se o valor da posição for menor, o processo é repetido, considerando que a lista tem a metade do tamanho e inicia da posição anterior. No caso do teste apresentado, em que se busca a vogal "o", a metade da lista está na posição 2, correspondendo ao valor "i", caso no qual será buscado no próximo elemento a partir da metade da lista. Assim, o valor "o" é encontradado na posição 3.
Que tal utilizar o emulador a seguir para testar as funções e praticar mais?
referências e links úteis
BANIN, S. L. Python 3 - conceitos e aplicações: uma abordagem didática. São Paulo: Érica, 2018.
CORMEN et. al. Introduction to algorithms. 2. ed. Cambridge: The MIT Press, 2001.
PSF - Python Software Fundation. Built-in Functions. 2020d. Disponível em: https://bit.ly/2XTVJmm. Acesso em: 10 mai. 2020.
STEPHENS, R. Essential algorithms: a practical approach to computer algorithms. [S. l.]: John Wiley & Sons, 2013.
TOSCANI, L. V; VELOSO, P. A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012.



