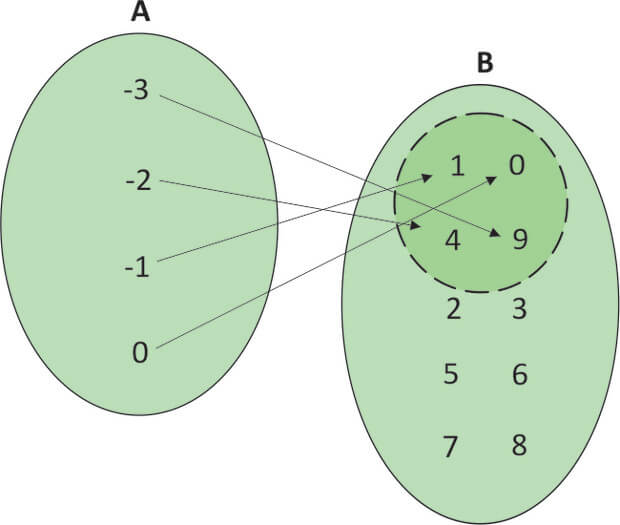
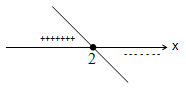
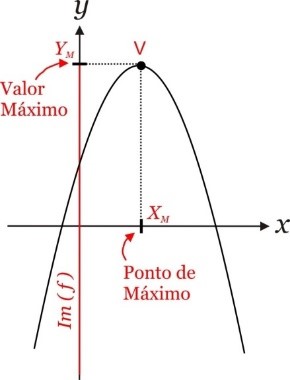
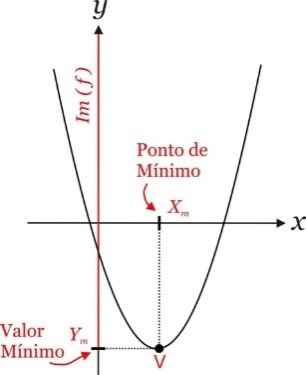
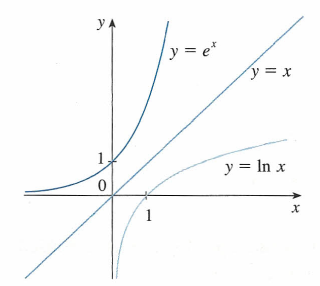
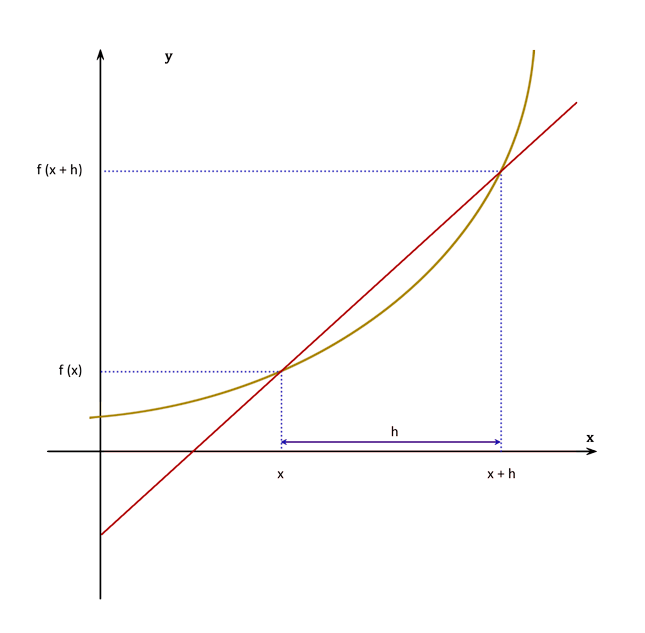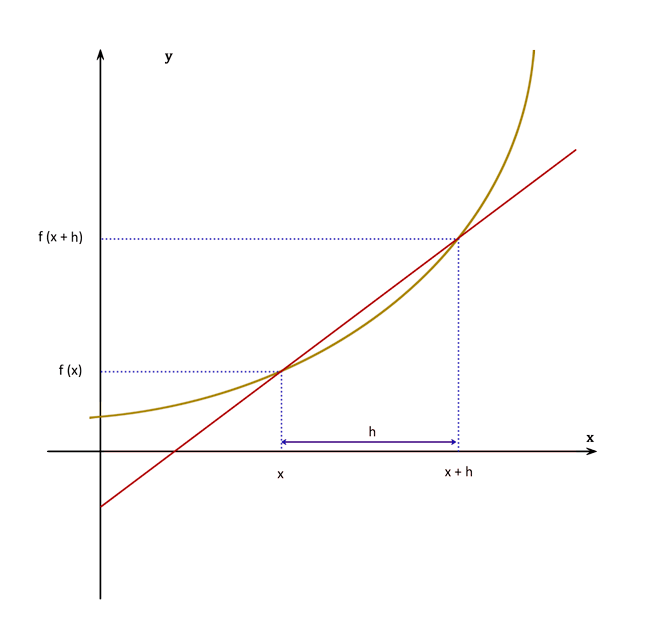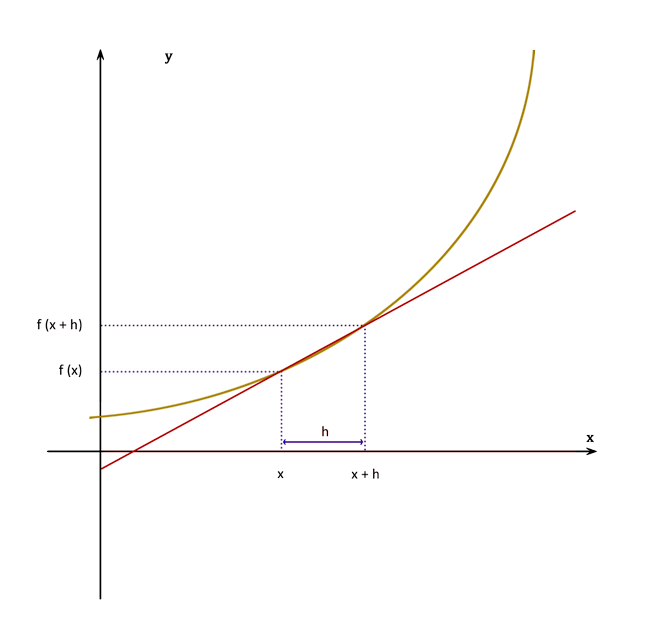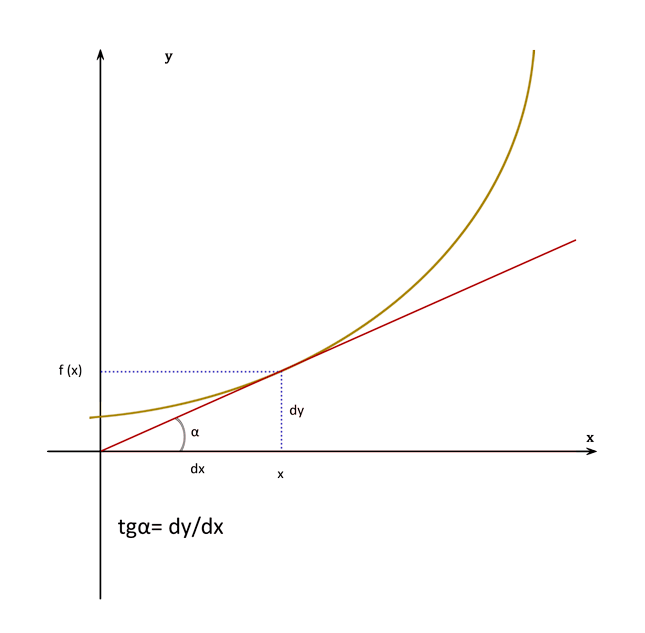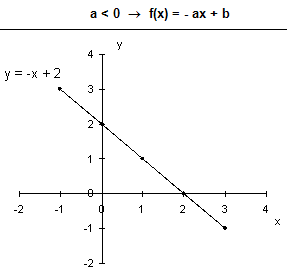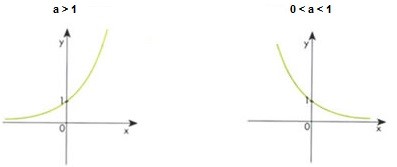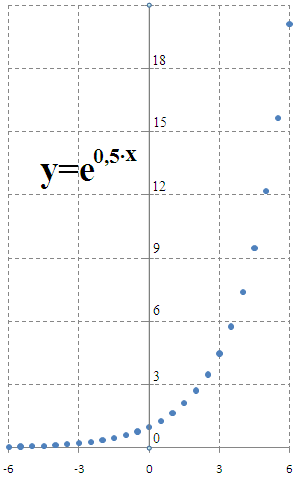Conteúdo Programático

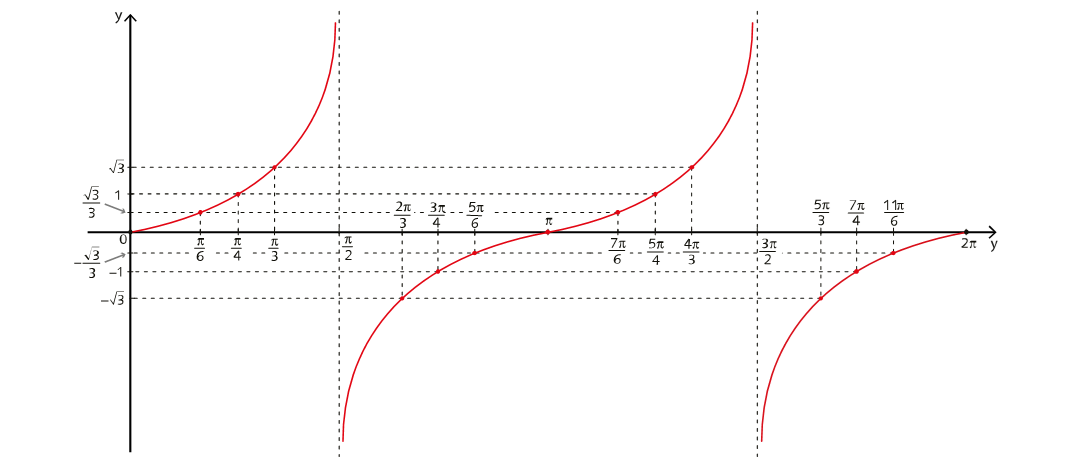
• Funções polinomiais, trigonométricas, exponenciais e logarítmicas.

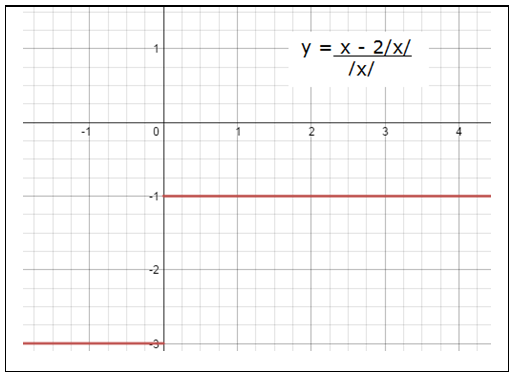
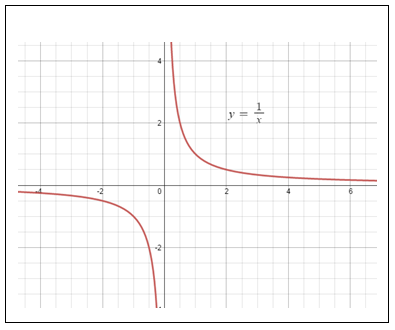
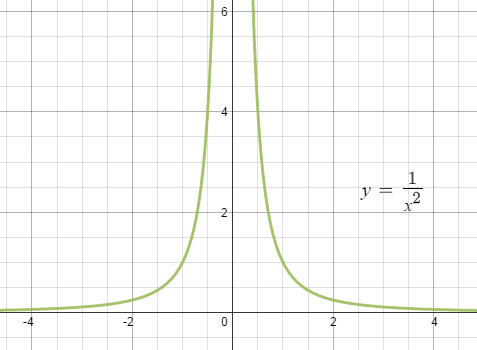
• Conceito de limite e limites fundamentais.

• Conceito de derivada e derivadas de funções polinomiais, exponenciais, logarítmicas e trigonométricas.

• Derivada da soma, do produto, do quociente e regra da cadeia.

Função, limite, derivada

Fonte: <https://goo.gl/crEkjx>. Acesso em: 24 out. 2017.

Apresentação da Webaula

O desenvolvimento do Cálculo no século XVII por Newton e Leibniz propiciou aos cientistas da época, as primeiras noções sobre "taxa de variação instantânea", tal como ocorre com a velocidade ou a aceleração. Esse conceito influenciou os métodos computacionais e os conhecimentos sobre Cálculo que se desenvolveram a partir do conceito de limites. Nessa aula estudaremos as diferentes funções apresentando seus conceitos, suas propriedades e exemplos. Todo desenvolvimento de cálculo está baseado no estudo de funções.

O estudo das funções, permite a você aluno adquirir a linguagem algébrica como a linguagem das ciências. Esta linguagem se faz necessária para expressar a relação entre grandezas e modelar situações-problema, construir modelos descritivos de fenômenos e permitir várias conexões dentro e fora da própria Matemática. O estudo de limites e derivada são muito importantes para a compreensão do Cálculo. Vamos então estudar o conceito e de limites, assim como o conceito de derivada e algumas regras de derivação.

Desenvolvimento do tema

Definindo uma função: Função é uma relação. Utilizando dois conjuntos A e B, a relação entre eles será uma função se todo elemento do primeiro conjunto estiver relacionado (ligado) apenas com um elemento do segundo conjunto. Na matemática, dizemos que função é uma relação de dois conjuntos, por exemplo: f(x) = y, sendo que x e y são valores, onde x é um elemento do domínio da função (a função está dependendo dele) e y é um elemento da imagem. Podemos citar como exemplo, a relação entre o custo e o consumo em m³ de água. Isso porque, a conta de água está relacionada a quanto iremos gastar de m³ de água. Essa relação é uma função!

Domínio, contradomínio e Imagem?

Seja f uma função de A em B.

Representação de função

Fonte: <https://goo.gl/EF7x16>. Acesso em 24 out. 2017.

Nesta correspondência, o conjunto A é o domínio da função f, enquanto o conjunto B é denominado contradomínio da função f.

Usamos a notação ⨏: A→B (onde lemos: f é uma função de A para B) para indicar que estamos fazendo a correspondência de A, designado domínio, com o conjunto B, contradomínio. Escrevemos y = ⨏(x) para indicar que a função f associa o elemento x de seu domínio ao elemento y de seu contradomínio.

• Se um elemento x ∈ A, for relacionado a um elemento y ∈ B, dizemos que y é a imagem de x pela função ⨏. Logo, o conjunto de todos os elementos de B, que são imagens de algum elemento de A, é designado conjunto imagem da função f é denotado por Im(⨏). Sendo portanto, um subconjunto do contradomínio B.

• O elemento x é chamado de variável independente, pois ele é livre para assumir qualquer valor do domínio, e nomeia-se y de variável dependente.

Tipos de funções

Seja $f$ uma função definida por $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{1} x + a_{0}$ , em que os coeficientes $a_{0}$ , $a_{1}$ ,... $a_{n}$ são números reais $(a_{n} \neq 0)$ e n um número inteiro não negativo. A função $f$ é denominada de função polinomial de grau n, a qual dependendo do grau n receberá nomes de funções polinomiais.

Podemos definir a função linear afim como uma aplicação $f : ℜ \to ℜ$ quando a cada elemento $x \in ℜ$ associa o elemento $a x + b \in ℜ$ onde $a \neq 0$ é um número real dado. Isto é, a função $f$ é dada por: $f (x) = a x + b, a \neq 0$

Analisar a função f(x) = – x + 2.

Fonte: Elaborado pelo autor.

Gráfico de uma função linear

Fonte: Elaborado pelo autor.

- A função é decrescente, pois a < 0;

- Coeficiente angular é a = -1;

- Coeficiente linear é b = 2;

- Zero da função é 2, pois – x + 2 = 0 => -x = - 2.(-1) => x = 2.

-A raiz 2 é a abscissa do ponto de coordenadas (2,0), a reta corta o eixo

f(x) < 0 {x ∈ R | x > 2}

f(x) = 0 {x ∈ R | x = 2}

f(x) > 0 {x ∈ R | x < 2}

Tipos de funções

A função quadrática, também nomeada função polinomial do 2º grau, é definida a partir de: f de R em R, dada na forma: f(x)=ax2+b+c com a, b e c pertencentes ao conjunto dos números reais, onde a ≠ 0. Vale salientar que o domínio desta função é o conjunto dos números reais e a representação de seu gráfico é a curva conhecida como parábola. Chamamos de raízes ou zeros da função polinomial do 2º grau dado por: f(x)=ax²+bx+c, a≠0, os números reais x que satisfazem f(x) = 0, ou seja, os valores da abscissa x que tornam y nulo. A descrição que nos permite obter as raízes é da forma:

$X = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ , tal representação é denominada como fórmula de bháskara.

Vértice de uma função quadrática

Fonte: <https://goo.gl/svWeZA>. Acesso em 16 mai. 2015.

Como representar o gráfico da função quadrática dada por y = -x2+2x+3.

I. Definindo a concavidade da parábola.

Temos a = -1, como a < 0 a concavidade para baixo.

II. ∆ pode ser obtido por ∆ = b²-4ac

∆ = (2)² - 4(-1)(3)

∆ = 4 + 12 = 16

III. Cálculo das raízes.

$x' = - \frac{b + \sqrt{Δ}}{2 a} e x " = - \frac{b - \sqrt{Δ}}{2 a}$

IV. Assim por meio de $X ν = - \frac{b}{2 a} e Y ν = - \frac{Δ}{4 a}$ encontramos o vértice V.

$X ν = - \frac{b}{2 a} e Y ν = - \frac{Δ}{4 a}$

Chama-se função exponencial a função f de R em R* apresentada pela forma característica, em que a é um número real positivo e diferente de um.

Definição: $f : R \overset{}{\to} R *$ ,com $f (x) = a^{x}$ é exponencial se a>0 e a≠1.

Função Exponencial

Fonte: <https://goo.gl/8e1Ki5>. Acesso em: 24 out. 2017.

Exemplo do gráfico da função exponencial

Fonte: <https://goo.gl/vsnyXD>. Acesso em 24 out. 2017.

$y = e^{0,5 x}$

Toda função que obedece a lei de formação $f : I R_{+}^{*} \to I R$ , definida por $f (x) = \log_{b} x$ , satisfazendo as condições de existências ( $0 < b \neq 1$ ) chamamos de função logarítmica. Na definição apresentada destacamos o domínio da função f que simbolicamente representamos por $D_{f} = R_{+}^{*}$ e a imagem que é dada por ${Im}_{f} = R$ .

Simbolicamente, temos: $\begin{array}{l} f : I R_{+}^{*} \to I R \\ x \to \log_{b} x \end{array}$

Exemplo: Qual o valor de $\log_{2} 16 = 4$ , pois se $\log_{2} 16 = x$ , então:

$2^{x} = 16$ temos então $2^{x} = 2^{4}$ , logo x=4, portanto $\log_{2} 16 = 4$ .

O logaritmo em base e é chamado de logaritmo natural de x, denotado por ln x e definido como sendo a função inversa de $e^{x}$ , ou seja, o logaritmo natural de x, escrito ln x, é a potência de e de necessária para obter x. Em outras palavras, lnx = c significa que $e^{c} = x$ . Veja que “e” é outra base para o logaritmo, que possui uma denominação especial, mas que possui exatamente as mesmas propriedades já apresentadas. A figura a seguir apresenta o gráfico da função exponencial $e^{x}$ e lnx.

Gráfico da função exponencial ex e sua inversa lnx

Fonte: Extraído de Stewart (2011, p. 56).

A função seno é a função $f : ℝ \to ℝ$ , dada por $f (x) = sen x$ , que associa a cada número real x, um único número $sen x$ , também real. Para construir o gráfico que representa a função seno no plano cartesiano, podemos atribuir alguns valores a x, a fim de obtermos os valores correspondentes para $y = f (x)$ . Com isso, obtemos os pares ordenados $(x, y)$ .

Gráfico da função $f (x) = sen x$

Fonte: Elaborado pelo autor.

A função cosseno é a função $g : ℝ \to ℝ$ , dada por $g (x) = \cos x$ , que associa a cada número real x um único número $\cos x$ , também real. Assim como no caso do seno, para construir o gráfico que representa a função cosseno no plano cartesiano, podemos atribuir alguns valores a x, a fim de obtermos os valores correspondentes para $y = g (x)$ . Com isso, obtemos os pares ordenados $(x, y)$ .

Gráfico da função $g (x) = \cos x$

Fonte: Elaborado pelo autor.

A função tangente é a função $h : ℝ \to ℝ$ , com $x \neq \frac{π}{2} + k π$ e $k \in ℤ$ , dada por $h (x) = tg x$ , que associa, a cada número real x, um único número $tg x$ , também real.

Gráfico da função $h (x) = tg x$

Fonte: Elaborado pelo autor.

Nesse gráfico, as retas tracejadas verticais são chamadas assíntotas e passam pelos pontos de abscissas $\frac{π}{2} + k π$ , com $k \in ℤ$ . Algumas características dessa função:

• É periódica e seu período é $π$ . Isso pode ser justificado observando que: $tg x = tg (x + k \cdot π)$ , com $k \in ℤ$

• O contradomínio é $ℝ$ , mas o domínio da função tangente é $D (h) = {x \in ℝ | x \neq \frac{π}{2} + k π, k \in ℤ}$ . No entanto, ao contrário das funções seno e cosseno, os valores de $tg x$ não estão restritos ao intervalo $[- 1, 1]$ , ou seja, $Im (h) = ℝ$ . Isso fica evidente na circunferência trigonométrica, pois os valores da tangente se estendem infinitamente para cima e para baixo sobre o eixo das tangentes.

Limites

Para compreendermos os limites vamos começar trabalhando a noção intuitiva. Seja a função f(x)=2x+1, vamos atribuir valores para “x’ que se aproximem de “1” por valores menores que 1(esquerda) e por valores maiores que 1(direita).

Noção intuitiva de limite

x

y=x2+1

1,5

4

1,3

3,6

1,1

3,2

1,05

3,1

1,02

3,04

1,01

3,02

x

y=x2+1

0,5

2

0,7

2,4

0,9

2,8

0,92

2,9

0,98

2,96

0,99

2,98

Fonte: Elaborado pelo autor.

Notamos que à medida que x se aproxima de 1, y se aproxima de 3, ou seja, quando x tende para 1 (x 1), y tende para 3 (y 3), ou seja:

\lim_{x \to l} (2 x + 1) = 3

Observamos que quando x tende para 1, y tende para 3 e o limite da função é 3. Esse é o estudo do comportamento de f enquanto x ->1, x não precisa assumir o valor 1. Se f(x) tende para 3 (f(x) 3), dizemos que o limite de f quando x 1 é 3. Podem ocorrer alguns casos em que para x = 1 o valor de f(1) não seja 3.

Definimos como limite de uma função f quando “x” tende a “c” e é representado pela notação $\lim_{x \to c} f (x)$ , como sendo o número L, tal que f(x) pode se tornar tão próxima a L quanto quisermos sempre que existir suficientemente próximo de “c”, com x≠c. Se existir escrevemos:

\lim_{x \to c} f (x) = L

Podemos analisar o limite considerando cada lado separado. Dizemos que o limite esquerdo de f quando “x” tende a “a” é igual a L se pudermos tornar os valores de f(x) próximos de L, tomando “x” suficiente próximo de a desde que “x” seja menor que “a”. Notação: $\lim_{x \to a -} f (x) = L$ . O símbolo x→a- indica que estamos considerando somente valores “x” menores que “a” e da mesma forma para x→a+ indica que estamos considerando valores maiores que “a”. Pela definição teremos:

\lim_{x \to a} f (x) = L \leftrightarrow \lim_{x \to a} - f (x) = L e \lim_{x \to a} + f (x) = L

Exemplo: Como determinar o limite de $\lim_{x \to c} \frac{x - 2 |x|}{|x|} = L$ ?

Vamos primeiro determinar o limite quando “x” tende a zero pela direita!

Para o módulo de um número positivo, teremos:

$\lim_{x \to 0} + \frac{x - 2 |x|}{|x|} = \lim_{x \to 0} + \frac{x - 2 x}{x} = \lim_{x \to 0} + \frac{- x}{x} = \lim_{x \to 0} (- 1) = - 1$

Determinando o limite quando “x” tende a zero pela esquerda!

Para o módulo de um número negativo, teremos -x, será o oposto do número:

Notação: $\lim_{x \to 0} - \frac{x - 2 |x|}{|x|} = \lim_{x \to 0} - \frac{x + 2 x}{- x} = \lim_{x \to 0} - = - 3$

Assim, se o limite pela direita é igual a -1 e pela esquerda é -3, talvez o limite “L” não se define, observe a representação gráfica:

Representação gráfica da função $y = \frac{x - 2 |x|}{|x|}$

Fonte: Elaborado pelo autor.

Percebe que no eixo vertical das ordenadas há uma lacuna entre os números -1 e -3 representando uma descontinuidade, na verdade o limite não se define.

Propriedades dos Limites

Muitas das propriedades de limites são utilizadas com objetivo de simplificar as resoluções de algumas funções:

Leis do Limite Seja c uma constante e suponha que existam os limites $\lim_{x \to a} f (x) e \lim_{x \to a} g (x)$

Então

1. $\lim_{x \to a} [f (x) + g (x)] = \lim_{x \to a} f (x) + \lim_{x \to a} g (x)$

"O limite de uma soma é a soma dos limites"

2. $\lim_{x \to a} [f (x) - g (x)] = \lim_{x \to a} f (x) - \lim_{x \to a} g (x)$

"O limite da diferença é a diferença dos limites"

3. $\lim_{x \to a} [c f (x)] = c \lim_{x \to a} f (x)$

"O limite de uma constante vezes uma função é a constante vezes o limite da função"

4. $\lim_{x \to a} [f (x) g (x)] = \lim_{x \to a} f (x) . \lim_{x \to a} g (x)$

"O limite de um produto é o produto dos limites"

5. $\lim_{x \to a} \frac{f (x)}{g (x)} = \frac{\lim_{x \to a} f (x)}{\lim_{x \to a} g (x)} s e \lim_{x \to a} g (x) \neq 0$

"O limite de um quociente é o quociente dos limites (Desde que o limite do denominador seja diferente de zero)"

6. $\lim_{x \to a} [f (x)]^{n} = [\lim_{x \to a} f (x)]^{n}$ onde n é um inteiro positivo

7. $\lim_{x \to a} c = c$

8. $\lim_{x \to a} x = a$

9. $\lim_{x \to a} x^{n} = a^{n}$ onde n é um inteiro positivo

10. $\lim_{x \to a} \sqrt[n]{x} = \sqrt[n]{a}$ onde n é um inteiro positivo [Se n for par, supomos que a>0]

11. $\lim_{x \to a} \sqrt[n]{f (x)} = \sqrt[n]{\lim_{x \to a} f (x)}$ onde n é inteiro positivo [Se n for par, supomos que $\lim_{x \to a} f (x) > 0$

Vejamos alguns casos para determinar o limite de uma função:

1) Determine o limite de $\lim_{x \to 0} \frac{1}{x}$ , com x≠0:

Representação gráfica da função $y = \frac{1}{x}$

Fonte: Elaborado pelo autor.

Podemos observar que:

• Quando x se aproxima de zero, pela direita, y cresce indefinidamente superando qualquer valor arbitrário que fixemos, isto é, y tende a mais infinito. $\lim_{x \to 0 +} \frac{1}{x} = \infty$

• Quando x se aproxima de zero, pela esquerda, y decresce indefinidamente, isto é, y tende a menos infinito. $\lim_{x \to_0} \frac{1}{x} = - \infty$

• Não existe $\lim_{x \to 0} f (x)$ porque os limites laterais são diferentes.

• Quando x cresce indefinidamente, o gráfico quase toca o eixo x, isto é, y tende a zero. $\lim_{x \to + \infty} \frac{1}{x} = 0$

• Quando x decresce indefinidamente, o gráfico quase encosta no eixo x, isto é, y tende a zero. $\lim_{x \to_\infty} \frac{1}{x} = 0$

2) Determine o limite de $\lim_{x \to 0} \frac{1}{x^{2}}$ , quando “x” tende a zero:

• Quando x cresce ou decresce indefinidamente, a função se aproxima de zero, ou seja, y tende a zero.

$\lim_{x \to + \infty} \frac{1}{x^{2}} = 0 \lim_{x \to_\infty} \frac{1}{x^{2}} = 0$

Quando x se aproxima de zero, y cresce indefinidamente, isto é, y tende a mais infinito. $\lim_{x \to 0} \frac{1}{x^{2}} = + \infty$

Fonte: Elaborado pelo autor.

3) Limite da função polinomial para x tendendo a mais ou menos infinito: $\lim_{x \to \infty} \frac{3 x^{2} - x - 2}{5 x^{2} + 4 x + 1} = ?$

Para calcular limites no infinito, primeiro dividimos o numerador e o denominador pela maior potência de x que ocorre no denominador. No nosso caso, a maior potência de x é x², então temos:

\lim_{x \to \infty} \frac{3 x^{2} - x - 2}{5 x^{2} + 4 x + 1} =

4) Cálculo de uma indeterminação do tipo $\frac{0}{0}$ . Exemplo: Calcular o limite de $\lim_{x \to 3} \frac{x^{2} - 9}{x - 3}$

Observe que $f (x) = \frac{x^{2} - 9}{x - 3}$ não é definida para x=3, e o numerador e o denominador da fração tendem a zero quando x se aproxima de 3.

Fatorando e simplificando, temos:

$\lim_{x \to 3} \frac{x^{2} - 9}{x - 3} = \lim_{x \to 3} \frac{(x + 3) (x - 3)}{x - 3} = \lim_{x \to 3} x + 3 = 3 + 3 = 6$

A aplicabilidade dos limites está associada ao cálculo de taxas de variações nas mais diversas áreas. Variação de tempo, acelereação, valores, são só alguns exemplos em que podemos uaar limites. A taxa de variação instantânea compreende um valor de variação num instante específico. No processo de se definir a taxa de variação instantânea, são consideradas taxas de variação médias em intervalos que vão diminuindo em torno de um ponto. Esse processo de tornar o tamanho do intervalo tão pequeno que se aproxime de zero, trata-se do cálculo do limite.

Derivada num ponto

Percebe-se que a derivada de uma função num ponto é a taxa de variação instantânea naquele ponto.

Taxa de variação de f em a = f' (a) = \lim_{h \to 0} \frac{f (a + h) - f (a)}{h} .

Se existir o limite, então f é diferenciável em a. Uma expressão bastante usada para tratar de derivadas das funções é “cálculo diferencial”. Verifique que se x = a + h, então h = x – a e h tende

f' (a) = \lim_{x \to a} \frac{f (x) - f (a)}{x - a} .

a 0 se e somente se x tende a “a”. Consequentemente, uma maneira equivalente de enunciar a definição da derivada é

Considere o exemplo extraído de Stewart (2010, p. 133) – Encontrar a derivada da função f(x) = x2 – 8x + 9 em um número “a”.

Solução: usando a definição de derivada em que h → 0, deve-se aplicar a f(x) que se deseja derivar. É importante lembrar que é necessário subtrair a função f(x) quando estiver no ponto x=a+h da f(x) quando x=a. Logo, algebricamente a solução é a descrita a seguir.

\begin{array}{l} f' (a) = \lim_{h \to 0} \frac{f (a + h) - f (a)}{h} \\ f' (a) = \lim_{h \to 0} \frac{[{(a + h)}^{2} - 8 (a + h) + 9] - [a^{2} - 8 a + 9]}{h} \\ f' (a) = \lim_{h \to 0} \frac{a^{2} + 2 a h + h^{2} - 8 a - 8 h + 9 a^{2} + 8 a - 9}{h} \\ f' (a) = \lim_{h \to 0} \frac{2 a h + h^{2} - 8 h}{h} = \lim_{h \to 0} (2 a + h - 8) \\ f' (a) = 2 a - 8 \end{array}

Há muitas notações usadas representar a derivada de uma função y = f(x). Além de f'(x), as mais comuns são:

f' (x) = y' = \frac{d y}{d x} = \frac{d f}{d x} = \frac{d}{d x} f (x) = D f (x) = D_{x} f (x) .

Os operadores D e d/dx são chamados operadores diferenciais, pois indicam a operação de diferenciação que é o processo de cálculo de uma derivada. dy/dx é lido como “a derivada de y em relação a x”, e df/dx ou (d/dx)f(x) como “a derivada de f em relação a x”.

As notações que indicam a derivada de uma função também podem indicar um ponto em que se deseja avaliar a derivada, como segue.

{y' |}_{x = a} o u {\frac{d y}{d x} |}_{x = a} o u {\frac{d}{d x} f (x) |}_{x = a} .

O símbolo de avaliação (|x=a) significa calcular a expressão à esquerda em x = a.

Agora que você já conhece as notações para as derivadas de funções, aprenderá algumas regras de derivação. Essas regras permitem calcular a derivada de uma função rapidamente.

Regra 1 – Derivada de uma função constante é zero.

$\frac{d}{d x} (c) = 0.$

Regra 2 – Derivada de uma função potência, quando n for um número real qualquer.

$\frac{d}{d x} (x^{n}) = n x^{n - 1} .$

Exemplo:

$f (x) = x^{5} \Rightarrow f' (x) = 5 . x^{5 - 1} \Rightarrow f' (x) = 5 x^{4}$

Regra 3 – Derivada de uma função multiplicada por constante.

$\frac{d}{d x} [c f (x)] = c \frac{d}{d x} f (x) .$

Exemplo:

$\begin{array}{l} f' (x) = \frac{d}{d x} 10 x^{3} \Rightarrow f' (x) = 10 \frac{d}{d x} x^{3} \Rightarrow f' (x) = 10.3 x^{3 - 1} \Rightarrow f' (x) = 30 x^{2} \\ f' (4) = {30.4}^{2} = 30.16 \Rightarrow f' (4) = 480. \end{array}$

Regra 4 – derivada da soma ou diferença de duas funções deriváveis.

$\frac{d}{d x} [f (x) \pm g (x)] = \frac{d}{d x} f (x) \pm \frac{d}{d x} g (x) .$

Calcule a derivada de f(x) = x2 – 8x + 9. Em seguida, determine a taxa de variação instantânea da função f(x) em x = 3.

Solução:

$\begin{array}{l} f' (x) = \frac{d}{d x} (x^{2} - 8 x + 9) \\ f' (x) = \frac{d}{d x} x^{2} - \frac{d}{d x} 8 x + \frac{d}{d x} 9 \\ f' (x) = \frac{d}{d x} x^{2} - 8 \frac{d}{d x} x + \frac{d}{d x} 9 \\ f' (x) = 2 x^{2 - 1} - 8 x^{1 - 1} + 0 \\ f' (x) = 2 x - 8 \\ f' (3) = 2.3 - 8 = - 2. \end{array}$

Definição da Regra da Cadeia

A regra da cadeia é a regra de derivação mais utilizada. Usamos esta regra quando a função a ser derivada é resultante da composição de outras funções. Dessa forma, a função composta f(g(x)) com f sendo a função de fora e g a função de dentro. Ou ainda,

z = g(x) e y = f(z), logo y = f(g(x)).

A regra da cadeia diz que a derivada de uma função composta é o produto das derivadas das funções de fora e de dentro, lembrando que a função de fora precisa ser calculada com a função de dentro.

A regra de cadeia poderá ser representada pela expressão matemática:

• [f(g(x))]’ = f’(z).g’(x) notação de linha

• $\frac{d y}{d x} = \frac{d y}{d z} . \frac{d z}{d x}$ notação de Leibniz

Vamos ver como funciona a regra da cadeia.

Exemplo 1: Determine a derivada da função y = (x² + 2)¹⁰⁰
Vamos considerar:
f(x) = (x² + 2)¹⁰⁰ e a sua derivada f(u) = u¹⁰⁰
g(x) = x² + 2 e a sua derivada g’(x) = 2x
Aplicando a Regra de Cadeia, teremos:
(f.g)’(x) = f’(g(x)).g’(x)
(f.g)’(x) = 100(x² +2) ⁹⁹. 2x
(f.g)’(x) = 200x (x² +2) ⁹⁹. 2x

Exemplo 2: Determine a derivada da função $y = e^{(2 x^{2} - 1)}$

Vamos considerar: $f (x) = e^{(2 x^{2} - 1)}$ a sua derivada $f (u) = e^{u}$

$g (x) = 2 x^{2} - 1$ e a sua derivada $g' (x) = 4 x$

Aplicando a Regra de Cadeia, teremos:

$(f . g)' (x) = f' (g (x)) . g' (x)$

Derivada de Função Logarítmica

Segundo (Anton et al 2014) estabelece-se que f(x) = ln x é diferenciável para x > 0 (ou seja, possui derivada em todos os pontos de x >0). A derivada do logaritmo natural é dada por:

\frac{d}{d x} (\ln x) = \frac{1}{x} .

Desse resultado segue que a derivada do logaritmo é dada por:

\begin{array}{l} \frac{d}{d x} (\log_{a} x) = \frac{d}{d x} (\frac{\ln x}{\ln a}) \\ \frac{d}{d x} (\log_{a} x) = \frac{1}{x \ln a}, x > 0. \end{array}

Veja um exemplo. Calcule a derivada da função y=ln (x2+1). Solução: Para resolver essa derivada será necessário usar a Regra da Cadeia estudada no tema anterior. Então vamos escrever a função y em termos de uma função composta:

y = f (z) = f (g (x)) = f (x^{2} + 1) = l n (x^{2} + 1) .

Dessa construção podemos dizer que y = f(g(x)), sendo z=g(x) e y= f(z) e a derivada pela regra da cadeia é: .

[f (g (x))]' = f' (z) . g' (x) ou \frac{d y}{d x} = \frac{d y}{d z} . \frac{d z}{d x}

$\begin{array}{l} Então tem-se: \\ z = x^{2} + 1, z' = \frac{d z}{d x} = 2 x, y = \ln z, y' = \frac{d y}{d z} = \frac{1}{z} \\ Substituindo os valores na fórmula da regra da cadeia: \\ \frac{d y}{d x} = \frac{d y}{d z} . \frac{d z}{d x} \Rightarrow \frac{d y}{d x} = \frac{1}{z} .2 x \Rightarrow \frac{d y}{d x} = \frac{1}{x^{2} + 1} .2 x \\ \frac{d y}{d x} = \frac{2 x}{x^{2} + 1} . \end{array}$

Derivada de função exponencial

A derivada da função f(x) = a^x pode ser definida de algumas formas. Observe como fica ao escrever x como logaritmo.

$\begin{array}{l} y = a^{x} \Rightarrow x = \log_{a} y dessa forma, é possível derivar os dois lados em relação a x \\ \frac{d}{d x} x = \frac{d}{d x} (\log_{a} y) pela regra de derivação de logaritmos, tem-se \\ 1 = \frac{1}{y \ln a} \frac{d y}{d x} \Rightarrow \frac{d y}{d x} = y \ln a como y = a^{x}, então ao substituir tem-se \\ \frac{d y}{d x} = a^{x} \ln a ou seja, essa é a derivada da função exponencial y = a^{x} . \end{array}$

No caso especial em que a base “a” é igual a “e” (a = e), e sabendo-se que ln e = 1, então a derivada de f(x) = e^x é f’(x) = ex.1 = e^x.

Derivada da função exponencial composta:

Se u(x) é uma função derivável, aplicando a regra da cadeia podemos generalizar as proposições:

$i) y = a^{u} (a > 0, a \neq 1) \to y' a^{u} . I n a . u'$

Veja um exemplo. Calcule a derivada da função y=(1/2)^√x. Solução: Para resolver essa derivada será necessário usar a Regra da Cadeia, como ocorreu no Exemplo 1. Então separar as funções menores que compõem a função y.

$\begin{array}{l} y = f (g (x)) \Rightarrow {\begin{cases} z = g (x) \\ y = f (z) \end{cases} \\ z = \sqrt{x} \Rightarrow z' = \frac{1}{2} x^{- \frac{1}{2}} \\ f (z) = {(\frac{1}{2})}^{z} \Rightarrow f' (z) = {(\frac{1}{2})}^{z} \ln \frac{1}{2} \end{array}$

Substituindo os valores na fórmula da Regra da Cadeia:

$\begin{array}{l} \frac{d y}{d x} = \frac{d y}{d z} \frac{d z}{d x} \\ y' = {(\frac{1}{2})}^{z} \ln \frac{1}{2} . (\frac{1}{2} x^{- \frac{1}{2}}) \\ Substituindo z e efetuando as operações matemáticas \\ y' = {(\frac{1}{2})}^{\sqrt{x}} \ln \frac{1}{2} . (\frac{1}{2} . \frac{1}{\sqrt{x}}) \\ y' = {(\frac{1}{2})}^{\sqrt{x}} \ln \frac{1}{2} . (\frac{1}{2 \sqrt{x}}) \end{array}$

Derivada das Funções Trigonométricas: sen x e cos x

A derivada para a função y = sen x é y’ = cos x. De forma análoga é possível chegar a derivada da função y = cos x é y´= - sen x. As demais funções trigonométricas são definidas a partir do seno e cosseno, podemos usar as regras de derivação para encontrar suas derivadas.

t g x = \frac{s e n x}{\cos x}; c o t g x = \frac{\cos x}{s e n x}; s e c x = \frac{1}{\cos x}; \cos s e c x = \frac{1}{s e n x}

Veja um exemplo:

S e y = t g x = \frac{s e n x}{\cos x}, e n t ã o y' = s e c^{2} x

Usando a regra do quociente, obtemos:

$y' = \frac{\cos x . \cos x - s e n x (- s e n x)}{\cos^{2} x}$

$= \frac{\cos^{2} x + s e n^{2} x}{\cos^{2} x}$

$= \frac{1}{\cos^{2} x} = \sec^{2} x$

Derivada das Funções Trigonométricas: sen x e cos x

De modo análogo, podemos encontrar:

Função

Derivada

y= cotg x

y`= - cosec²x

y= sec x

y´= sec x. tg x

y= cosec x

y´= - cossec x. cotg x

Usando a regra da cadeia, obtemos as formas gerais das derivadas.

Função

Derivada

y= senx

y= cos x. x´

y= cosx

y= -sem x. x´

y= tgx

y =sec²x. x´

y= cotgx

y= -cossec²x. x´

y= cotgx

y`= -cosec²x

y= secx

y´= sec x. tg x. x´

y= cosecx

Y´= - cossec x. cotg x. x´

Assista

Veja a seguir alguns links sobre os temas estudados nesse texto.

Funções

https://www.youtube.com/watch?v=ot8n4I64A38

https://www.youtube.com/watch?v=Pt0ev9GpJJg

https://www.youtube.com/watch?v=DGy6CYTag8I

Limites

https://www.youtube.com/watch?v=o94j-PVi9gA

https://www.youtube.com/watch?v=wDltsMh8CCw

https://www.youtube.com/watch?v=MRdxIZYykJk

Derivada

https://www.youtube.com/watch?v=oAzEQLUUmp4

https://www.youtube.com/watch?v=op7ZXBTkDwA

https://www.youtube.com/watch?v=DFspBukQfdU

https://www.youtube.com/watch?v=2N9O6OW10D0

https://www.youtube.com/watch?v=wvW1txFfqJg

https://www.youtube.com/watch?v=DFMDQ9lTx4g

https://www.youtube.com/watch?v=7oHKPyNSWc4

Referências e Dicas de Leitura

HUGHES-HALLETT, Deborah. Cálculo de uma Variável. 1ª ed. Rio de Janeiro: LTC - Livros Técnicos e Científicos, 2009. PLT 178.

ANTON, Howard. Cálculo – volume I, 8ª Edição. Bookman, 2007

HUGHES-HALLET, Deborah; McCALLUM, William G.; GLEASON, Andrew M. et al. Cálculo - A Uma e a Várias Variáveis - Vol. 1, 5ª edição. LTC, 2011 <https://goo.gl/hb6MUz>. Acesso em 03 de março de 2015.

HOFFMANN, Laurence D.; BRADLEY, Gerald L. Cálculo - Um Curso Moderno e suas Aplicações - Tópicos Avançados, 10ª edição. LTC, 2010 <https://goo.gl/VkktAo>. Acesso em 3 de março de 2015.

Referências e Dicas de Leitura

ÁVILA, Geraldo Severo de Souza; ARAÚJO, Luís Cláudio Lopes de. Cálculo - Ilustrado, Prático e Descomplicado. LTC, 2012 <https://goo.gl/EAV9bE>. Acesso em 3 de março de 2015.

ANTON, Howard. BIVENS, Irl. Davis, Stephen. Cálculo. 8º ed. São Paulo:Bookman, 2007<https://goo.gl/PCEG3C>. - Acesso em 3 de março de 2015.

MALTA, Iaci. PESCO, Sinésio. LOPES. Hélio. Cálculo de uma variável. 3º ed. Rio de Janeiro:PUC-RIO, 2007. Vol II. <https://goo.gl/fSncV1>. - Acesso em 3 de março de 2015.

Referências e Dicas de Leitura

MUROLO, Afrânio Carlos; BONETTO, Giácomo. Matemática Aplicada a Administração, Economia e Contabilidade. 2ª ed. São Paulo: Cengage Learning, 2012.

STEWART, J. Cálculo I. V. 01. 5ª ed. São Paulo:Cengage Learning, 2008.

Nome do Professor

Título Card Capa

Unidade 1 - Seção 1

Sub-título da capa interna

Teoria de controle moderno

Webaula 1

Fundamentos de funções, limites e derivadas

Conteúdo Programático

Apresentação da Webaula

Desenvolvimento do tema

Tipos de funções

Tipos de funções

Limites

Propriedades dos Limites

Derivada num ponto

Definição da Regra da Cadeia

Derivada de Função Logarítmica

Derivada de função exponencial

Derivada da função exponencial composta:

Derivada das Funções Trigonométricas: sen x e cos x

Derivada das Funções Trigonométricas: sen x e cos x

Assista

Referências e Dicas de Leitura

Referências e Dicas de Leitura

Referências e Dicas de Leitura

Bons estudos!